リーマンテンソル

リーマンテンソル(Schutz1985)、また、Riemann-Christoffel曲率テンソル(Weinberg1972,p.133;Arfken1985,p.123)またはRiemann曲率テンソル(Misner et al. 1973,p.218)は、一般相対性理論において有用な四指数テンソルである。 リッチ曲率テンソルとスカラー曲率がの項で定義できるような他の重要な一般相対論的テンソル。

リーマンテンソルは、ある意味で計量テンソルとその第一および第二の導関数から構成できる唯一のテンソルです,

(1)

ここで、は第一種のクリストッフェル記号であり、はカンマ導関数である(Schmutzer1968,p.108;Weinberg1972)。 ある次元では、＜５ ７ ０ ０＞Ｒ＿（１ １ １ １）＝０＜７ ６ ６ ２＞である。 4つの次元では、256の部品があります。 対称性の関係を利用して,

(2)

独立したコンポーネントの数は36に削減されます。 条件の使用

(3)

座標の数は21に減少します。 最後に、を使用して

(4)

20 独立した成分が残されている（Misner et al. 1973,pp.220-221;Arfken1985,pp.123-124)。

一般に、次元の独立成分の数は次のように与えられます

(5)

“四次元ピラミッド数”は、その最初のいくつかの値は次のとおりです0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415)。 とから構築できるスカラーの数は次のとおりです

(6)

(ワインバーグ1972）。 最初のいくつかの値は次のとおりです0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297)。

ヤコビテンソル,

(7)

しましょう

(8)

ここで、内の量は、第二種のクリストッフェル記号です。 その後

(9)

次元で最も単純な分解に分解されます,

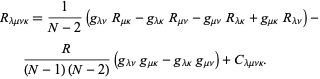(10)

ここで、はリッチ曲率テンソル、はスカラー曲率、はワイルテンソルである。