Ornstein-Uhlenbeck進化の下で最適を推定する
Michael R.May
最後に変更された月16, 2019
進化的最適の推定
このチュートリアルでは、最適な表現型が時間校正された系統発生の枝の間で一定であると仮定されるOrnstein-Uhlenbeckモデルを指定する方法を示しています(missing reference)から脊椎動物のクレード間の(log)体サイズのデータセットを使用して(missing reference)。 このチュートリアルでは、各コンポーネントの確率的グラフィカルモデル表現を提供します。 モデルを指定した後、マルコフ連鎖モンテカルロ(MCMC)を使用してOrnstein-Uhlenbeck進化のパラメータを推定します。
Ornstein-Uhlenbeckモデル
単純なOrnstein-Uhlenbeck(OU)モデルの下では、連続文字は最適値theta theta.に向かって進化すると仮定されます。 文字は、ドリフトパラメータsigma\sigma^2.に従って確率的に進化します。 文字は、適応率、alpha\alpha alphaによって最適に向かって引っ張られます。; alphaの値が大きいほど、文字がtheta theta.に向かってより強く引っ張られていることを示します。 文字がtheta\theta.から離れるにつれて、パラメータalpha\alpha.は文字がどれだけ強く引き戻されるかを決定します。 このため、alpha\alpha.は”rubber band”パラメータと呼ばれることがあります。 適応率パラメータalpha alpha=0.の場合、OUモデルはBMモデルに崩壊します。 連続した文字の確率は系統発生(このチュートリアルでは既知であると仮定します)と三つのOUパラメータ()にのみ依存するため、結果のグラフィカルモデ
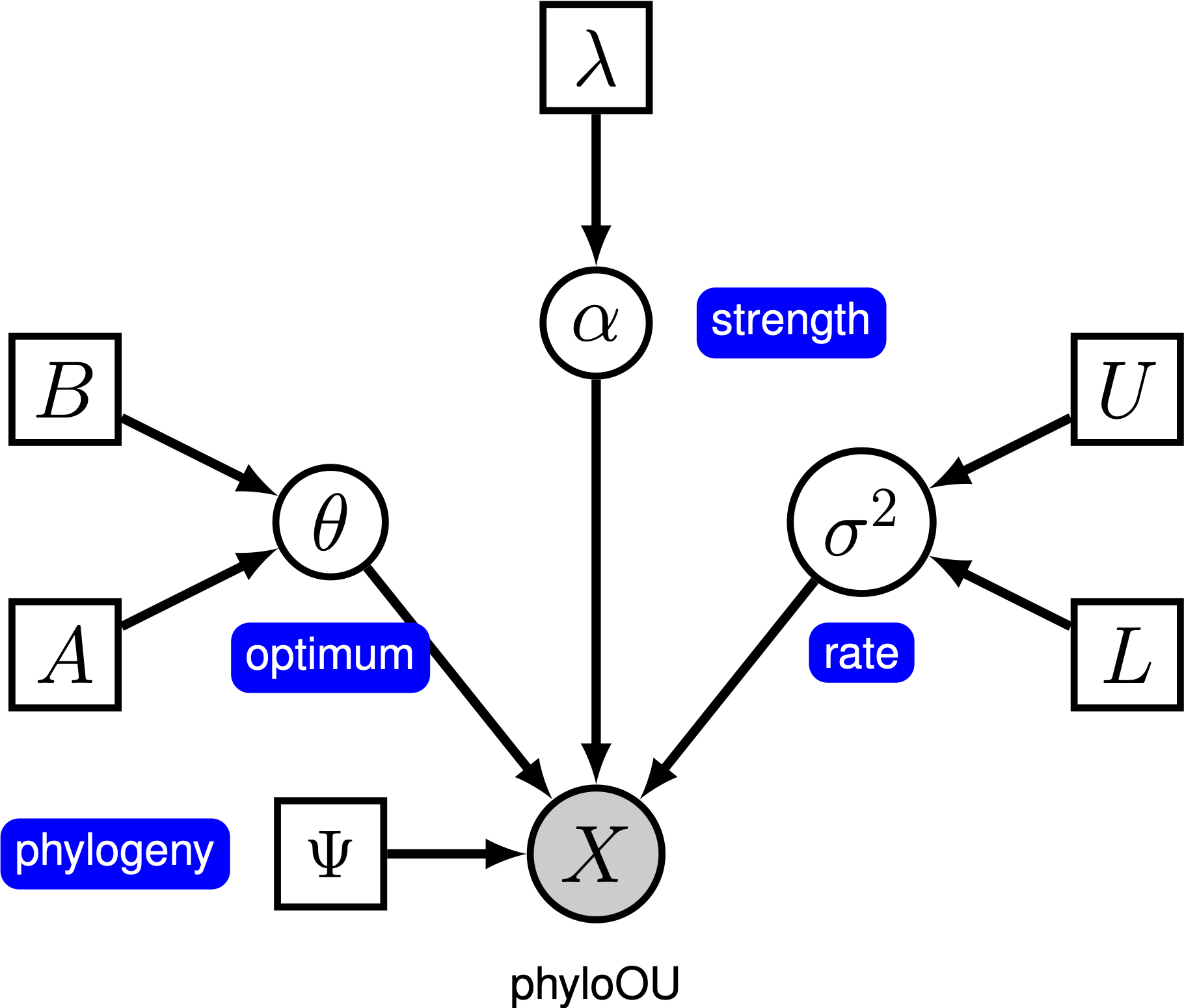
このチュートリアルでは、(Landis and Schraiber2017)の66の脊椎動物の系統発生と(ログ)ボディサイズのデータセットを使用します。
⇨完全なOUモデル仕様はmcmc_OU.Revという名前のファイルにあります。
データを読み込む
まず、66個の脊椎動物のデータセットのうち、どのデータセットを使用するかを決定します。 ここでは、最初のデータセット(Acanthuridae)を分析していると仮定しますが、任意のデータセットを自由に選択する必要があります。
dataset <- 1ここで、選択したデータセットに対応する(時間校正された)ツリーを読み取ります。
T <- readTrees("data/trees.nex")次に、同じデータセットの文字データを読み込みます。
data <- readContinuousCharacterData("data/traits.nex")さらに、vector ofmovesとmonitorsの変数を初期化します:
moves = VectorMoves()monitors = VectorMonitors()モデルの指定
ツリーモデル
このチュートリアルでは、ツリーが面積なしで既知であると仮定します。 観察された系統発生に対応するツリーの定数ノードを作成します。
tree <- Tレートパラメータ
進化の確率率は、レートパラメータsigma sigma^2.によって制御されます。 我々は、loguniform priorからレートパラメータを描画します。 これは対数スケールで一様であり、これは速度の大きさのオーダーについての無知を表していることを意味する。
sigma2 ~ dnLoguniform(1e-3, 1)sigma\sigma^2.の事後分布を推定するには、このノードで動作するMCMC提案メカニズムを提供する必要があります。 Sigma sigma^2.はレートパラメータであり、したがって正でなければならないため、mvScaleと呼ばれるスケーリング移動を使用します。
moves.append( mvScale(sigma2, weight=1.0) )適応パラメータ
最適に向かって適応率は、パラメータalpha alpha.によって決定されます。 指数関数的な事前分布からalpha\alpha.を描画し、その上にスケール提案を配置します。
alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )Optimum
-10から10までの漠然としたユニフォームの前から最適値を描画します(キャラクターがこの範囲外にある場合は、この前に変更する必要があります)。 このパラメータは正または負になる可能性があるため、スライド移動を使用してMCMC中の変更を提案します。
theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )Ornstein-Uhlenbeckモデル
モデルのパラメータを指定したので、対応する系統発生OUモデルから文字データを描画できます。 この例では、REMLアルゴリズムを使用して尤度を効率的に計算します(Felsenstein1985)。 文字は、ツリーのルートで最適な値で始まると仮定します。
X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)observed X$が観測されたデータ()であることに注意して、dataをこの確率的ノードにクランプします。
X.clamp(data)最後に、model()を使用してモデル全体のworkspaceオブジェクトを作成します。 ワークスペースオブジェクトは=演算子で初期化され、それ自体がベイズグラフィカルモデルの一部ではないことを覚えておいてください。 model()関数は、モデルグラフ全体を走査し、指定したモデル内のすべてのノードを検索します。 このオブジェクトは、単一のDAGノードではなく、モデルオブジェクト全体を参照する便利な方法を提供します。
mymodel = model(theta)MCMC分析の実行
モニターの指定
MCMC分析では、マルコフ連鎖の状態を記録するモニターのベクトルを設定する必要があります。 モニター関数はすべてmn*と呼ばれ、*はモニターの種類を表すワイルドカードです。 まず、mnModel関数を使用してモデルモニターを初期化します。 これにより、MCMC関数に渡されたときにすべてのモデルパラメーターの状態を出力する新しいモニター変数が作成されます。
monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )さらに、指定された変数の状態をmnScreenで画面に報告する画面モニターを作成します:
monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )MCMCシミュレーション
を初期化して実行するには、完全に指定されたモデル、モニターのセット、および移動のセットを使用して、wecanは今、事後確率に比例 mcmc()関数はMCMCオブジェクトを作成します:
mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")今、MCMCを実行します:
mymcmc.run(generations=50000)分析が完了すると、監視対象のファイルが出力ディレクトリにあります。
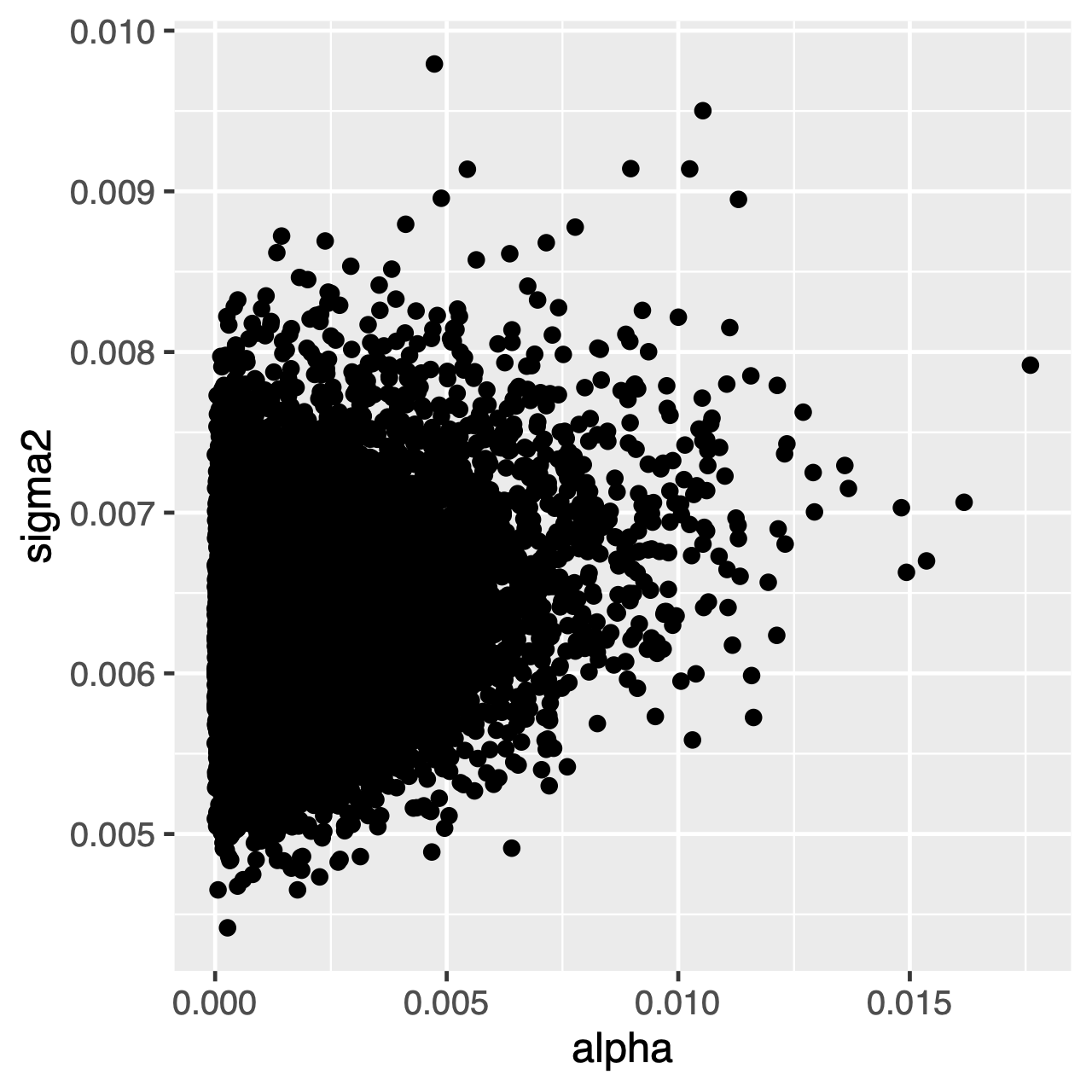
▼この分析を実行するためのRevファイル: OUプロセスの下で進化する文字は、平均theta\theta.と分散variance\sigma^2\div2\alpha.を持つ正規分布である定常分布に向かう傾向があります。 したがって、進化率が高い(またはツリー内の枝が比較的長い)場合、process\sigma^2.とalpha\alpha.を別々に推定することは困難です。process\sigma^2.とalpha\alpha.は両方ともプロセスの長期分散を決定 これが解析に影響するかどうかは、Tracerのパラメータの関節後方分布を調べることによって確認できます。 パラメータが正の相関関係にある場合は、それらの周辺分布を解釈することを躊躇する必要があります(つまり、適応率または分散パラメータについて別々に推論しないでください)。
1
- MCMCシミュレーションを実行して、OU最適値の事後分布を推定します(
theta)。 - 生成された出力ファイルを
Tracerにロードします:thetaの平均事後推定値と推定HPDとは何ですか? -
Tracerを使用して、alphaとsigma2の関節後方分布を比較します。 これらのパラメータは相関しているか、または相関していませんか? - 前の平均と後の平均を比較する。 (ヒント:関数
mymcmc.run()でオプションの引数underPrior=TRUEを使用してください)それらは異なっていますか(例:)? 事後平均は、前の95%確率区間の外側にありますか?
OUモデルとBMモデルの比較
BMモデルとOUモデルの両方に適合できるようになったので、どのモデルがよりよく適合するかを自然に知りた このセクションでは、可逆ジャンプマルコフ連鎖モンテカルロを使用してOUモデルとBMモデルの適合を比較する方法を学びます。
可逆ジャンプMCMCを使用したモデル選択
キャラクターが選択的最適に向かって進化するという仮説をテストするために、2つのモデルを想像します。 最適化への適応がない最初のモデルは、alpha alpha=0.の場合です。 2番目のモデルは、alpha alpha>0.のOUモデルに対応しています。 これは、ブラウン運動が適応率が0のときのOUモデルの特別な場合であるために機能します。 残念ながら、alpha\alpha.は連続パラメータであるため、標準マルコフ連鎖は各値が正確に0に等しい状態を訪問することはありません。 幸いなことに、可逆ジャンプを使用して、マルコフ連鎖がブラウン運動モデルを訪問することを検討できるようにすることができます。 これには、2つのモデルのそれぞれに事前確率を指定し、OUモデルにprior\alpha.の事前分布を提供することが含まれます。
rjMCMCを使用すると、マルコフ連鎖は事後確率に比例して二つのモデルを訪問することができます。 モデルi i.の事後確率は、チェーンがそのモデルを訪問していたサンプルの割合にすぎません。 モデルにpriorも指定しているため、OUモデルのベイズ係数を次のように計算できます。
\
ここで、P P(\text{ouモデル}\mid X)andとP P(\text{ouモデル}))は、ouモデルの事後確率
OuモデルとBMモデル間の可逆ジャンプ
rjMCMCを有効にするには、関連するパラメータalpha alpha.の前に可逆ジャンプを配置するだけです。 Prior onalphaを変更して、定数値0を取るか、事前分布から引き出されるようにすることができます。 最後に、p = 0.5のOUモデルで事前確率を指定します。
alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)次に、二つのモデル間の変更を提案するalpha上の可逆ジャンプ提案を提供します。
moves.append( mvRJSwitch(alpha, weight=1.0) )さらに、MCMCがOUモデルを訪問しているときのための通常のmvScale提案を提供します。
moves.append( mvScale(alpha, weight=1.0) )チェーンがOUモデルを訪問しているときに1の値を持つ変数と、BMモデルを訪問しているときに1の値を持つ対応する変数を含めます。 これにより、このパラメータの事後平均値を計算するだけで済むため、モデルの事後確率を簡単に計算できます。
is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)is_OU = 1がOUモデルの事後確率であるサンプルの割合。 あるいは、この指標変数の事後平均推定値は、OUモデルの事後確率に対応します。 これらの値は、上記のベイズ因子方程式で使用して、いずれかのモデルのベイズ因子サポートを計算できます。
- Felsenstein J.1985. 系統発生と比較方法。 アメリカの自然主義者。:1-15.10.1086/284325
- Höhna S.,Heath T.A.,Boussau B.,Landis M.J.,Ronquist F.,Huelsenbeck J.P.2014. 系統発生学における確率的グラフィカルモデル表現。 体系的な生物学。 63:753-771.10.1093/sysbio/syu039
- Landis M.J.,Schraiber J.g.2017. 脈打った進化は現代の脊椎動物の体の大きさを形作った。 国立科学アカデミーの学位を取得している。 114:13224-13229.10.1073/1710920114