또한,이 곡률 텐서(와인버그 1972,피.133;아프 켄 1985,피.123)또는 리만 곡률 텐서(미스너 외)로 알려진 리만 텐서(슈츠 1985,피.7545,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피.5586,피. 1973,피.218)는 일반 상대성 이론에 유용한 4 인덱스 텐서. 리치 곡률 텐서와 스칼라 곡률의 관점에서 정의 할 수있는 다른 중요한 일반 상대 론적 텐서
.
리만 텐서는 어떤 의미에서 미터법 텐서와 그 첫 번째 및 두 번째 파생물에서 구성 할 수있는 유일한 텐서입니다,
 |
(1)
|
감마는 첫 번째 종류의 크리스토펠 기호이고
는 쉼표 파생물입니다(슈무처 1968,피.108;와인버그 1972). 한 차원에서
. 네 가지 차원에서 256 개의 구성 요소가 있습니다. 대칭 관계의 만들기 사용,
 |
(2)
|
독립적 인 구성 요소의 수는 36 로 줄어 듭니다. 조건 사용
 |
(3)
|
좌표 수는 21 로 줄어 듭니다. 마지막으로,사용
 |
(4)
|
20 독립적 인 구성 요소가 남아 있습니다(미스너 외. 1973,220-221 쪽;아프 켄 1985,123-124 쪽).
일반적으로,
차원에 있는 독립적인 성분의 수는 곁에 주어집니다
 |
(5)
|
“4 차원 피라미드 숫자”의 처음 몇 값은 다음과 같습니다 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (2002415). 의 수는 스칼라에서 건설할 수 있
및
가
 |
(6)
|
(Weinberg1972). 처음 몇 값은 다음과 같습니다 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … 2018 년 10 월 15 일
측면에서의 야곱은 텐서
,
 |
(7)
|
하자
 |
(8)
|
여기서내부의 양은 두 번째 종류의 크리스토펠 상징이다. 그런 다음
 |
(9)
|
차원에서 가장 간단한 분해로 분해,
 |
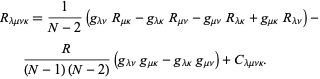(10)
|
여기서은 리치 곡률 텐서,
은 스칼라 곡률,
은 바일 텐서이다.