hvis du har lest forrige innlegg om hva som er en induktans, la oss gå videre til neste nivå, hva er induktansformelkretsene.
Nå som induktoren er lagt til i vår liste over passive elementer, er det nødvendig å utvide det kraftige verktøyet for serie-parallell kombinasjon. Vi trenger å vite hvordan vi finner ekvivalent induktans av et seriekoblet eller parallellkoblet sett med induktorer funnet i praktiske kretser.
Serie Induktorer
Vurder en serieforbindelse Av n induktorer, som vist i Figur.(1a), med ekvivalent krets vist I Fig.(1b).

induktorene har samme strøm gjennom dem. Bruke KVL til løkken,

Erstatte vk= Lk di / dt resultater i
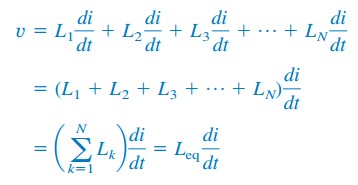
hvor

Dermed,
den ekvivalente induktansen til seriekoblede induktorer er summen av de individuelle induktansene.
Induktorer i serie kombineres på nøyaktig samme måte som motstander i serie.
Parallelle Induktorer
vi vurderer nå en parallell tilkobling Av n induktorer, som vist i Figur.(2a), med ekvivalent krets I Fig.(2b). Induktorene har samme spenning over dem. Ved HJELP AV KCL,

Men


derfor

hvor
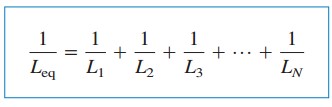
den innledende strømmen i (t0) Gjennom Leq ved t= t0 forventes AV KCL å være summen av induktorstrømmene ved t0. Således, I Henhold Til Ligning.(5),
![]()
I Henhold Til Ligning.(6),
den ekvivalente induktansen til parallelle induktorer er den gjensidige av summen av de gjensidige av de individuelle induktansene.
Merk at induktorene parallelt kombineres på samme måte som motstander parallelt.
For to induktorer parallelt (N = 2), Ligning.(6) blir
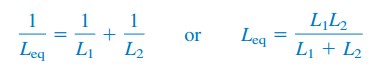
Induktans Formel Kretser Eksempler
1. Finn ekvivalent induktans av kretsen vist i Fig.(3).
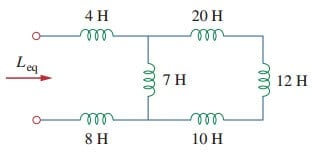
Løsning:
10-H, 12-H og 20-H induktorer er i serie; dermed kombinerer dem gir en 42-H induktans. Denne 42-h induktoren er parallell med 7-H induktoren slik at de kombineres for å gi


Denne 6-h-induktoren er i serie med 4-H-og 8-h-induktorene. Derfor,
![]()
2. For kretsen I Fig.(4),
i (t) = 4 (2−e-10t) mA. Hvis i2(0) = -1 mA, finn:
(a) i1(0);
(b) v(t), v1(t) og v2(t);
(c) i1(t) og i2(t).

Løsning:
(a) fra i (t) = 4 (2−e-10t) mA, i(0) = 4(2 − 1) = 4 mamma.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(c) den nåværende i1 er oppnådd som


På Samme Måte,


Merk at i1 (t) + i2 (t) = i (t).