Riemann Tensor

Riemann tensor(Schutz 1985) , også kjent Riemann-Christoffel kurvatur tensor (Weinberg 1972, s. 133; Arfken 1985, s.123) Eller Riemann kurvatur tensor (Misner et al. 1973, s. 218), er en fire-indeks tensor som er nyttig i generell relativitet. Andre viktige generelle relativistiske tensorer slik At Ricci kurvatur tensor og skalar kurvatur kan defineres i form av .

Riemann tensor er på en måte den eneste tensor som kan konstrueres fraden metriske tensor og dens første og andre derivater,

(1)

hvor Er Christoffel symboler av den første typen og er et kommaderivat (Schmutzer 1968, s. 108; Weinberg 1972). I en dimensjon, . I fire dimensjoner er det 256 komponenter. Å gjøre bruk av symmetri relasjoner,

(2)

antall uavhengige komponenter reduseres til 36. Bruke tilstanden

(3)

antall koordinater reduseres til 21. Til slutt bruker

(4)

20 uavhengige komponenter er igjen (Misner et al. 1973, s. 220-221; Arfken 1985, s. 123-124).

generelt er antall uavhengige komponenter i dimensjoner gitt av

(5)

de «fire-dimensjonale pyramidale tallene», de første få verdiene er 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Antall skalarer som kan konstrueres fra og er

(6)

(Weinberg 1972). De første verdiene er da 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).

i forhold Til Jacobi tensor ,

(7)

La Oss

(8)

hvor mengden inne i er Et Christoffel-symbol av den andre typen. Deretter

(9)

Brutt ned i sin enkleste nedbrytning i dimensjoner,

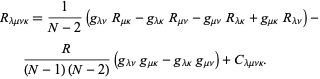(10)

Her Er Ricci kurvatur tensor, er skalar kurvatur, og Er Weyl tensor.