waarschijnlijk de meest gebruikte waarde in een bodemrapport is bodemdragende capaciteit. De voor de hand liggende reden is dat basisvoorbeelden in de meeste tekstboeken bijna altijd draagvermogen gebruiken om de plandimensie van een voet te berekenen. Vanwege de eenvoud en het gebruiksgemak is deze methode nog steeds de fundamentele bodemparameter voor funderingsontwerp. Echter, die eenvoud neemt de basis zal zich gedragen als een star lichaam. Die bijzondere aanname werkt goed in de praktijk voor kleine en enkele kolom voetstukken. Maar voor grote en multi-column funderingen geven de meeste ingenieurs de voorkeur aan flexibele analyse. Handmatige berekening van flexibele analyse kan een uitdaging zijn en, in bijna alle gevallen, softwareprogramma ‘ s zoals STAAD, SAFE, GT STRUDL etc. worden gebruikt. Echter, deze computerprogramma ‘ s vragen vaak om een input genaamd “modulus van subgrade reactie”. Veel ingenieurs zijn niet bekend met deze term en vaak proberen om het te vergelijken met draagvermogen. Aangezien steeds meer ingenieurs software zullen gebruiken om stichtingen te ontwerpen, is het essentieel voor ingenieurs om een fundamenteel inzicht te hebben in deze bodemparameter. Is er een verband tussen draagvermogen en modulus van subgrade reactie?
Modulus van de Subgradreactie (Ks)
deze term wordt gemeten en uitgedrukt als belastingsintensiteit per verplaatsingseenheid. Voor het Engelse eenheidssysteem wordt het vaak uitgedrukt in kip/in2/in; in het SI-systeem wordt het uitgedrukt als kN/m2/m. sommige drukken deze term uit in kip/in3 (of kN/m3), wat misleidend kan zijn. Numeriek is kip/in3 correct, maar geeft niet goed de fysische betekenis van de gemeten waarde weer en kan worden verward als een dichtheidseenheid of een volumetrische meting.
wiskundig wordt de coëfficiënt van de ondergradreactie uitgedrukt als:
Ks = p / s (Eqn 1)
waarbij p = contactdrukintensiteit en s = bodembezetting
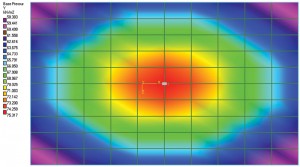
figuur 1a: Afbuigschema en bodemdrukcontour.
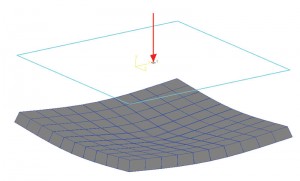
figuur 1b: bodemdrukcontour.
zoals Terzaghi al zei, kan een goede schatting van de contactdruk voor een flexibele fundering zeer omslachtig zijn, zodat wordt aangenomen dat Ks constant blijft voor de gehele fundering. Met andere woorden, de verhouding tussen druk en nederzetting op alle plaatsen van een voet zal constant blijven. Dus het verplaatsingsdiagram van een voet met een belasting in het midden zal een dishing effect hebben. Een punt in het midden van de voet zal de hoogste verplaatsing ervaren. Verplaatsing vermindert als het zich van het centrum verwijdert. Figuur 1a toont een eenvoudige slab-on-grade fundering. Het werd gemodelleerd en geanalyseerd in STAAD Foundation als “Mat”, dat is een flexibele fundering; de bodem werd gedefinieerd met behulp van coëfficiënt van subgrade reactie. Voor deze oefening werd de standaardwaarde van de software voor de modulus van de subgrade reactie gebruikt. Het verplaatsingsdiagram toont een dishing effect zoals eerder besproken. Figuur 1b toont de bodemdrukcontour. Het is ook duidelijk dat de drukintensiteit in het centrum maximaal is en vermindert naarmate de elementen (of knooppuntcoördinaten) zich van het centrum verwijderen. Er kan dus worden aangenomen dat de verhouding tussen drukintensiteit en afwikkeling constant is.
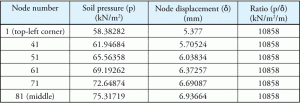
Tabel 1: bodemdruk, nodeverplaatsing en hun verhouding.
overweeg enkele getallen uit hetzelfde voorbeeld. De bodemdruk, de bijbehorende verplaatsing en de verhouding staan vermeld in Tabel 1. De punten worden op een diagonaal weergegeven om de variatie van druk en verplaatsing te illustreren als de punten zich van het centrum naar het verste punt in de hoek van de rechthoekige voet bewegen. Figuur 2 toont de punten op de matplaat.
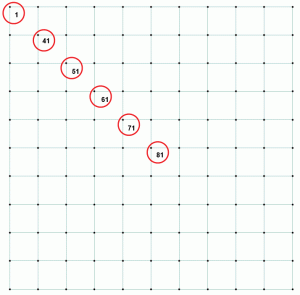
Figuur 2: Geselecteerde punten om basisdruk, doorbuiging en verhouding te vergelijken.
dit is nauwelijks een verrassing, omdat per definitie de modulus van de subgrade reactie (Ks) een constante is voor de gehele bodem en het programma Ks als grondeigenschap gebruikte. Het is ook belangrijk om op te merken dat de standaardwaarde van de software Ks (10858 kN/m2/m) exact dezelfde was als de constante verhouding berekend in Tabel 1.
de basisdruk werd berekend aan de hand van de ondersteuningsreactie. Men zou kunnen denken dat de verhouding van steunreactie en overeenkomstige verplaatsing ook een constante zal zijn. Zoals blijkt uit Tabel 2, zijn de verhoudingen niet constant voor alle waarden. Hoe wordt de KS-waarde binnen het programma gebruikt en hoe wordt de basisdruk berekend?
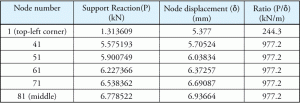
Tabel 2: ondersteunende reactie en verplaatsing.
zijrivier
vaak wordt verondersteld hoeveel oppervlakte van een plaat kan worden toegeschreven aan een knoop of, met andere woorden, de invloed van elke knoop op het oppervlak van een plaat. Het hangt af van de vorm van de plaat. Voor een perfecte vierkante of rechthoekige plaat zal elke knoop precies ¼ van het plaatoppervlak beïnvloeden (figuur 3a). Maar voor een veralgemeende vierhoek zou de beste praktijk zijn om het middelpunt van de massa van de plaat te berekenen en dan lijnen te tekenen van dat middelpunt naar de middelste punten van elke zijde. In Figuur 3b vertegenwoordigt het gearceerde gebied de invloedsoppervlakte van de corresponderende knoop.
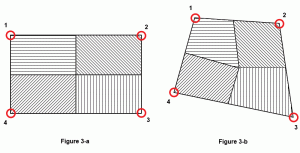
Figuur 3: knooppuntgebied.
veerconstante
de hierboven beschreven berekening van het zijrivieroppervlak is de belangrijkste intern door de commerciële software gebruikte methode om de lineaire veerconstante te berekenen. Het programma berekent eerst het zijriviergebied voor elke knoop van de voet en vermenigvuldigt dan de modulus van subgrade Reactie door het overeenkomstige zijriviergebied voor elke knoop om de lineaire veerconstante bij elke knoop te krijgen.
Kyi = Ks x Tai (Eqn 2)
waar
Kyi is de veerconstante bij i-node
Tai is de invloed gebied van i-node
Ks is de modulus van subgrade reactie
Voor een betonnen fundering analyse, die in de veren worden gedefinieerd als een compressie-alleen, zoals beton wordt verondersteld niet te dragen trekkracht. De basisdruk wordt berekend op elk steunknooppunt door de steunreactie te delen met het overeenkomstige knooppunt zijriviergebied. Als we naar het bovenstaande voorbeeld kijken, heeft knooppunt 1 een veel kleiner zijriviergebied dan de rest van de knooppunten. Het kan ook worden opgemerkt dat alle andere knooppunten hebben dezelfde zijrivier gebied. Dit verklaart Tabel 2, omdat het laat zien dat de verhouding voor knooppunt 1 anders is dan andere knooppunten. Figuur 4 toont het zijriviergebied voor verschillende knooppunten. Knooppunt 1 heeft een zijriviergebied dat 25% van knooppunt 81 is. Tabel 3 is een uitbreiding van de tabellen 1 en 2 en laat zien hoe een constante ratio wordt bereikt voor alle knooppunten.
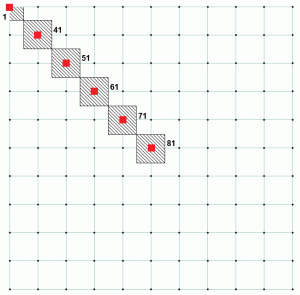
Figuur 4: Zijriviergebied van geselecteerde knooppunten.
toelaatbare nederzetting
draagvermogen is de meting van de bodemdruk die een bodem veilig kan dragen. Met andere woorden, draagvermogen is de druk die de bodem kan weerstaan voordat het uitvalt. De twee belangrijkste criteria voor bodemuitval zijn::
- Shear failure
- maximaal toelaatbare afwikkeling
onder vele factoren kan funderingsbreedte (B) faalcriteria beïnvloeden. Normaal, schuin falen regelt voor kleinere stichtingen en nederzetting falen regelt Grotere stichtingen. Tabel 4 is een typisch voorbeeld dat de relatie tussen verschillende funderingsgroottes en failure criteria laat zien.
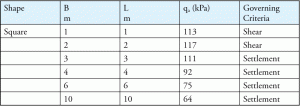
Tabel 4: definitief toelaatbaar draagvermogen voor toelaatbare afwikkeling = 25 mm en een bepaalde inbeddiepte.
voor het schatten van afwikkelingsfouten wordt uitgegaan van een toelaatbare afwikkelingswaarde (normaal 25 mm of 1 inch). Wanneer de grond meer neerzet dan de toegestane waarde, faalt de grond. Dus, zelfs voor een berekening van het draagvermogen, een toegestane bodembezetting wordt gebruikt en bouwkundig ingenieurs moeten zich bewust zijn van die waarde bij het ontwerpen van een voet. De toegestane bodembezettingswaarde is doorgaans een integraal onderdeel van een bodemrapport.
Waarom gebruik maken van de Modulus van de Ondergradreactie
eerder werd gesteld dat Voor het ontwerpen van een flexibele matfundering de modulus van de ondergradreactie wordt gebruikt in plaats van het draagvermogen van de bodem. Maar waarom? Het antwoord ligt in de onderliggende veronderstellingen van hoe een stichting zich zou kunnen gedragen.
stichtingen kunnen stijf of flexibel zijn. Draagvermogen wordt gebruikt om stijve funderingen te ontwerpen, maar de ondergrondreactie wordt gebruikt voor flexibele funderingen. De eigenlijke aanname van een starre fundering is dat “de verdeling van de subgrade reactie p over de basis van de fundering vlak moet zijn, omdat een starre fundering vlak blijft wanneer deze zich vestigt.”Beschouw een eenvoudig ondersteunde bundel geladen in het midden, zoals weergegeven in de figuur 5a. door statics, kunnen we R1 = P/2 en R2 = P/2. Als dezelfde bundel excentrisch wordt geladen, kan de reactie worden berekend zoals weergegeven in Figuur 5b.
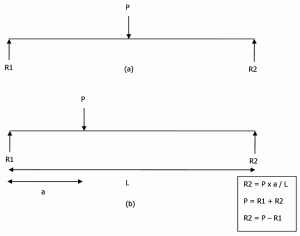
Figuur 5: Reacties voor een eenvoudig ondersteunde straal.
hetzelfde concept wordt uitgebreid voor Star funderingsontwerp. Maar in plaats van het einde ondersteunt, wordt de hele Stichting ondersteund. Ook wordt aangenomen dat de relatieve stijfheid van de betonplaat veel hoger is dan de bodemstijfheid. Dus, de plaat wordt verondersteld vlak te blijven, zelfs na het aanbrengen van de belasting.
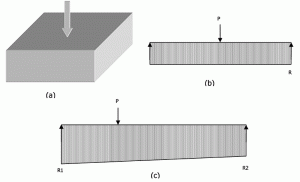
Figuur 6: subgrade reacties voor een geïsoleerde positie.
figuur 6a toont een voet in het midden. Uit een stijve brede bundel analogie, P = R X L. Evenzo, voor een excentrisch geladen voet, zal de reactie lineair variëren van het ene uiteinde naar het andere zoals weergegeven in Figuur 6c. vergelijkingen 3 en 4 kunnen worden opgelost om eindreacties te vinden. Maar geen van de vergelijkingen bevat modulus van subgrade reactie (Ks). Dus, de” verdeling van de subgradreactie op de basis van een starre basis is onafhankelijk van de mate van samendrukbaarheid van de subgrade ” waarop zij rust. Zoals veel auteurs hebben geconcludeerd, kan een stijve fundering veilig worden ontworpen met behulp van draagvermogen, omdat in de meeste gevallen deze methode meer conservatieve resultaten oplevert.
P = 1 / 2L (R1 + R2) (Eqn 3)
P x a = 1/6B2R1 + 1/3B2R2 (Eqn 4)
maar een matfundering is vaak ontworpen als een flexibele fundering omdat deze groot van grootte kan zijn en er veel belastingspunten en andere complexiteiten kunnen zijn, waaronder gaten en grade balken. Wijdverspreide beschikbaarheid van FEA-software draagt bij aan deze trend. Maar in tegenstelling tot starre funderingen kan een flexibele fundering geen lineaire subgradereactie hebben. Integendeel, het hangt af van de samendrukbaarheid van de stichting en de structurele stijfheid. Een flexibele fundering wordt onderworpen aan interne buiging en relatieve verschuivingen tussen twee plakpunten. Hoe groter de structurele stijfheid, hoe minder de relatieve verplaatsing. De auteur testte de behuizing met een zeer hoge stijfheid van de plaatelementen, resulterend in een bijna vlak oppervlak na het aanbrengen van de belasting. Evenzo, hoe groter de modulus van de subgrade reactie, hoe minder de drukverdeling. Met andere woorden, een hogere KS-waarde absorbeert meer druk op het laadpunt. Vandaar dat de modulus van de subgrade reactie,die de functie van bodembezetting en de externe druk is, wordt gebruikt voor flexibel funderingsontwerp.
correlaties
het meest voorkomende – en waarschijnlijk het veiligste-antwoord op de vraag van de correlatie tussen draagvermogen en de modulus van de subgradreactie is dat er geen correlatie is. Maar er moet een, als beide zijn de metingen van de bodemcapaciteit en een van deze twee parameters kan worden gebruikt om een regelmatige basis te ontwerpen.
ook hier is de definitie van Ks de druk per unit settlement. Met andere woorden, bodemcapaciteit om druk te weerstaan voor een bepaalde verplaatsing. Uit eerdere discussies is ook duidelijk dat zelfs draagvermogen een aanvaardbare oplossing heeft. Het is daarom verleidelijk om te concluderen dat de modulus van de subgradreactie het draagvermogen per unit settlement is.
deze conclusie lijkt sterk op de vergelijking van Bowles.
SI: Ks = 40 (SF)qa kN/m3(Eqn 5)
FPS: Ks = 12 (SF)qa k/ft3 (Eqn 6)
waarbij SF = veiligheidsfactor en qa het toelaatbare draagvermogen is.
in de vergelijkingen 5 en 6 wordt het toelaatbare draagvermogen eerst omgezet in het uiteindelijke draagvermogen door vermenigvuldiging met een veiligheidsfactor. De auteur ging uit van een inch of 25 mm schikking. De uiteindelijke vergelijking wordt dan geformuleerd, waarbij het uiteindelijke draagvermogen wordt gedeeld door de veronderstelde schikking.
de meer algemene vorm van de vergelijking kan worden geschreven als:
Ks = 
stress/verplaatsing (Eqn 7)
waar
I = veiligheidsfactor
qa is de toegestane draagvermogen
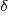is de toegestane bodem nederzetting
Deze vergelijkingen geven duidelijk aan dat de veiligheids-factor gebruikt moet worden, en de Ks-waarde beter kan worden vergeleken met de uiteindelijke draagkracht in plaats van de toegestane draagvermogen. De veiligheidsfactor kan variëren afhankelijk van projecten en geotechnische ingenieurs. De andere belangrijke factor is de veronderstelde toelaatbare verrekening voor het berekende draagvermogen.
ook moet worden opgemerkt dat de basisdrukwaarden die door de FEA-analyse worden gerapporteerd, niet rechtstreeks met het draagvermogen kunnen worden vergeleken. De maximale basisdruk moet worden vermenigvuldigd met de veiligheidsfactor en vervolgens worden vergeleken met het toegestane draagvermogen van de bodem.
de bovengenoemde vergelijkingen hebben echter beperkingen. Ze kunnen worden toegepast op funderingen waar afwikkelingsfout van toepassing is, maar kunnen niet worden gerelateerd aan funderingen waar afschuiffout optreedt voordat de toegestane afwikkelingslimiet wordt bereikt. Ingenieurs moeten dus voorzichtig zijn voordat ze deze vergelijkingen gebruiken.
conclusie
de correlatie tussen draagvermogen en modulus van de subgradreactie is in het beste geval een schatting. Het kan worden gebruikt voor de schatting, maar een Ks-waarde die door een plaatbelastingstest wordt bepaald, moet altijd worden gebruikt indien beschikbaar of indien mogelijk worden aangevraagd. Echter, de bovenstaande discussie geeft inzicht in deze waarden en helpt ingenieurs om de fysieke betekenis van modulus van subgrade reactie te begrijpen. En, zoals altijd, structurele ingenieurs moeten een geotechnisch ingenieur professional te raadplegen voordat de definitieve bodem stijfheid en lagerwaarden.▪