Ik ben begonnen met Andrew Ng ‘ s populaire machine learning cursus op Coursera. De eerste week omvat veel, in ieder geval voor iemand die al een paar jaar niet veel calculus heeft aangeraakt
- Kostenfuncties (gemiddelde verschil in het kwadraat)
- Gradiëntafdaling
- lineaire regressie
deze drie onderwerpen waren veel om in te nemen. Ik zal het hebben over elk in detail, en hoe ze allemaal in elkaar passen, met een aantal python code om te demonstreren.
4 mei bewerken: Ik publiceerde een follow-up gericht op hoe de kosten functie werkt hier, met inbegrip van een intuïtie, hoe het te berekenen met de hand en twee verschillende Python implementaties. Ik kan gradiëntafdaling doen en ze dan snel bij elkaar brengen voor lineaire regressie.
Modelrepresentatie
Ten eerste is het doel van de meeste machine learning-algoritmen om een model te construeren: een hypothese die kan worden gebruikt om Y te schatten op basis van X. de hypothese, of model, koppelt inputs aan outputs. Stel dat ik bijvoorbeeld een model train op basis van een aantal huisvestingsgegevens die de grootte van het huis en de verkoopprijs bevatten. Door een model te trainen, kan ik je een schatting geven van hoeveel je je huis kunt verkopen op basis van zijn grootte. Dit is een voorbeeld van een regressieprobleem — gegeven wat input, willen we een continue output voorspellen.
de hypothese wordt gewoonlijk gepresenteerd als

de theta-waarden zijn de parameters.
enkele snelle voorbeelden van hoe we de hypothese visualiseren:
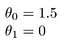
dit levert h ( x) = 1,5 + 0x op. 0x betekent geen helling, en y zal altijd de constante 1.5 zijn. Dit ziet eruit als:

Hoe zit het met
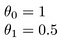

Het doel van het maken van een model is om te kiezen parameters, of theta-waarden, zodat h(x) dicht bij y voor de training data, x en y. Dus voor deze gegevens
x =
y =

Ik zal proberen een lijn van de beste pasvorm met behulp van lineaire regressie te vinden. Laten we beginnen.
kostenfunctie
we hebben een functie nodig die de parameters over onze dataset minimaliseert. Een veel voorkomende functie die vaak wordt gebruikt is gemiddelde kwadraat fout, die het verschil tussen de schatter (de dataset) en de geschatte waarde (de voorspelling) te meten. Het ziet er zo uit:

het blijkt dat we de vergelijking een beetje kunnen aanpassen om de berekening op het spoor een beetje eenvoudiger te maken. We eindigen met:
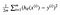
laten we deze const-functie toepassen op de volgende gegevens:

voor nu zullen we enkele Theta-waarden berekenen en de kostenfunctie met de hand plotten. Aangezien deze functie door (0, 0) gaat, kijken we slechts naar een enkele waarde van theta. Vanaf hier, zal ik verwijzen naar de kosten functie als J (Θ).
voor J (1) krijgen we 0. Geen verrassing — een waarde van J (1) levert een rechte lijn op die perfect bij de gegevens Past. Wat dacht je van J (0.5)?

de MSE functie geeft ons een waarde van 0.58. Laten we onze beide waarden tot nu toe plotten:
J(1) = 0
J (0,5) = 0.58

ik ga verder en bereken wat meer waarden van J (Θ).

en als we de punten mooi bij elkaar voegen…

we kunnen zien dat de kosten functie is op een minimum wanneer theta = 1. Dit is logisch — onze eerste gegevens is een rechte lijn met een helling van 1 (de Oranje Lijn in de figuur hierboven).
Gradiëntafdaling
we minimaliseerden J (Θ) door vallen en opstaan hierboven — gewoon veel waarden uitproberen en de resulterende grafiek visueel inspecteren. Er moet een betere manier zijn? Verloop afdaling in wachtrij. Gradiëntafdaling is een algemene functie voor het minimaliseren van een functie, in dit geval de functie gemiddelde kwadraat Foutkosten.
Gradiëntafdaling doet eigenlijk gewoon wat we met de hand deden – wijzig de theta waarden, of parameters, beetje bij beetje, totdat we hopelijk een minimum hebben bereikt.
we beginnen met het initialiseren van theta0 en theta1 naar elke twee waarden, zeg 0 voor beide, en gaan vanaf daar. Formeel is het algoritme als volgt:

waarbij α, alfa, de leersnelheid is, of hoe snel we naar het minimum willen gaan. Als α echter te groot is, kunnen we overshoot.

het geheel samenbrengen-lineaire regressie
snel samenvatten:
we hebben een hypothese:

die we moeten aanpassen aan onze trainingsgegevens. We kunnen een kostenfunctie zoals gemiddelde kwadraat fout gebruiken:

die we kunnen minimaliseren met gradiëntafdaling:

wat ons leidt naar ons eerste machine learning algoritme, lineaire regressie. Het laatste stukje van de puzzel dat we moeten oplossen om een werkend lineair regressiemodel te hebben is het gedeeltelijke derivaat van de kostenfunctie:
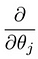
Waar blijkt te zijn:
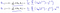
Dat geeft ons lineaire regressie!
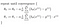
met de theorie uit de weg, ga ik verder met het implementeren van deze logica in python in de volgende post.
Edit 4 mei: Ik heb een vervolg gepubliceerd dat focust op hoe de kostenfunctie hier werkt, inclusief een intuïtie, hoe het met de hand te berekenen en twee verschillende Python implementaties. Ik kan gradiëntafdaling doen en ze dan snel bij elkaar brengen voor lineaire regressie.