des huizes Transformatie
des huizes Transformatie (ook de “heer des huizes Reflectie”) is een orthogonale transformatie reflectie:
- het reflex de vectoren in de kolommen van de matrix zo dat
- de eerste vector heeft alle nullen, behalve het eerste element
De Transformatie Matrix
Reflectie transformatie:
Eigenschappen
des huizes matrices symmetrische en orthogonaal: het zijn reflectiematrices
afleiding
dus we hebben $P = I-2vv^T$:
Wij gebruik van dergelijke transformaties voor nul elementen
QR Decomposition
Zoals in het geval van de LU Decompositie, waar we toegepast in een serie van Gauss Transformatie verandert, wij kunnen hetzelfde doen en het uitvoeren van een reeks van Gezinshoofd Transformaties
- dus als wij selecteren $y = \pm e_1$ (waar $e_1$ is de matrix met een 1 op positie 1 en de rest nullen)
- dan zal het zero alle elementen van $x$, behalve de eerste
- dus door de juiste keuze van het $H$ kunnen we $A$ en nul alle sub-diagonaal elementen
- kan dat meerdere keren voor elke kolom van $A$
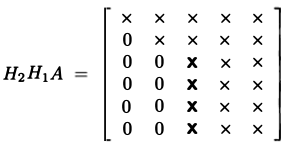
op Deze manier kunnen we het uitvoeren van QR Decomposition:
Hessenberg Ontleding
in Plaats van het gebruik van het voor terugdringing van de matrix, driehoek, die we kunnen gebruiken als Gezinshoofd Transformatie om een matrix te Hessenberg Matrix