proste modele Ornstein-Uhlenbeck

estymat Evolutionary Optima

ten poradnik pokazuje, jak określić model Ornsteina-Uhlenbecka, w którym zakłada się, że optymalny fenotyp jest stały wśród gałęzi filogenezy skalibrowanej w czasie (brak odniesienia), wykorzystując zbiory danych (log) wielkości ciała w obrębie kladów kręgowców z (brak odniesienia). W tym samouczku udostępniamy probabilistyczną graficzną reprezentację modelu każdego komponentu. Po określeniu modelu oszacujemy parametry ewolucji Ornsteina-Uhlenbecka za pomocą łańcucha Markowa Monte Carlo (MCMC).

Model Ornsteina-Uhlenbecka

w prostym modelu Ornsteina-Uhlenbecka (OU) zakłada się, że znak ciągły ewoluuje w kierunku optymalnej wartości, $\theta$. Znak ewoluuje stochastycznie zgodnie z parametrem dryfu, $ \ sigma^2$. Postać jest przyciągana do optimum przez szybkość adaptacji, $ \ alpha$; większe wartości Alfy wskazują, że znak jest przyciągany silniej w kierunku $\theta$. Gdy znak oddala się od $ \ theta$, parametr $ \ alpha$ określa jak mocno znak jest wycofywany. Z tego powodu parametr $ \ alpha$ jest czasami określany jako parametr „gumka”. Gdy parametr szybkości adaptacji $ \ alpha = 0$, model OU zwija się do modelu BM. Otrzymany model graficzny jest dość prosty, ponieważ prawdopodobieństwo ciągłych znaków zależy tylko od filogenezy (którą Zakładamy, że jest znana w tym tutorialu) i trzech parametrów OU ().

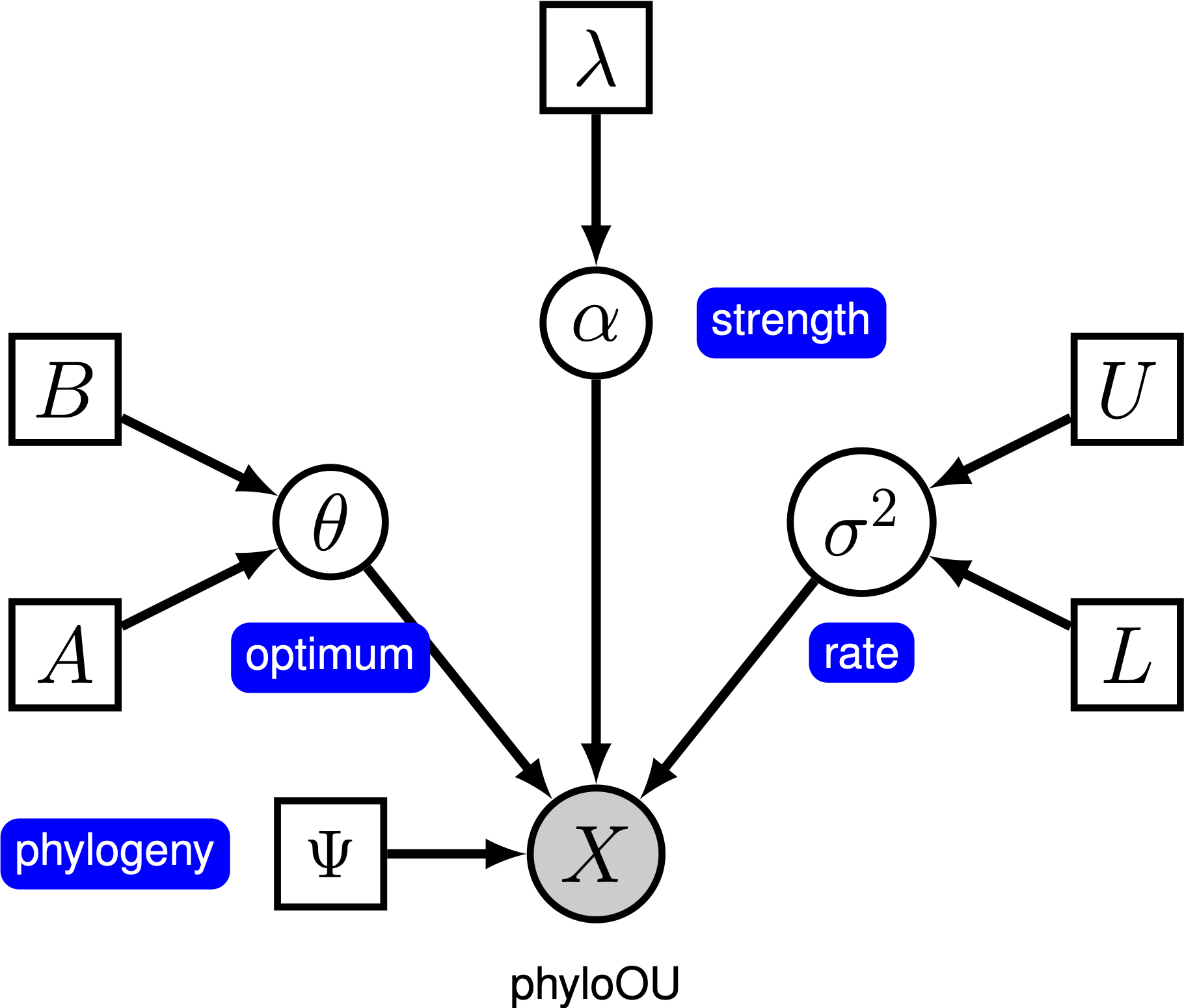
w tym poradniku używamy 66 filogenezy kręgowców i (log) body-size datasets z (Landis and Schraiber 2017).

full pełna specyfikacja modelu znajduje się w pliku o nazwie mcmc_OU.Rev.

Czytaj dane

zaczynamy od decyzji, który z 66 zestawów danych użyć. Tutaj Zakładamy, że analizujemy pierwszy zbiór danych (Acanthuridae), ale powinieneś wybrać dowolny z zestawów danych.

dataset <- 1

teraz czytamy w drzewie (skalibrowanym czasowo) odpowiadającym naszemu wybranemu zestawowi danych.

T <- readTrees("data/trees.nex")

następnie odczytujemy dane znakowe dla tego samego zbioru danych.

data <- readContinuousCharacterData("data/traits.nex")

dodatkowo inicjujemy zmienną dla naszego wektora i monitorów:

moves = VectorMoves()monitors = VectorMonitors()

określanie modelu

model drzewa

w tym samouczku Zakładamy, że drzewo jest znane bez obszaru. Tworzymy stały węzeł dla drzewa, który odpowiada obserwowanej filogenezie.

tree <- T

parametr Rate

stochastyczna szybkość ewolucji jest kontrolowana przez parametr rate, $ \ sigma^2$. Parametr rate rysujemy z loguniform prior. Przeor ten jest jednorodny w skali logarytmicznej, co oznacza, że oznacza ignorancję rzędu wielkości szybkości.

sigma2 ~ dnLoguniform(1e-3, 1)

aby oszacować tylny rozkład $\sigma^2$, musimy dostarczyć mechanizm propozycji MCMC, który działa na tym węźle. Ponieważ $ \ sigma^2$ jest parametrem rate i dlatego musi być dodatni, używamy ruchu skalowania o nazwie mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

parametr adaptacji

szybkość adaptacji do optimum jest określona przez parametr $ \ alpha$. Rysujemy $ \ alpha$ z wykładniczego rozkładu poprzedzającego i umieszczamy na nim propozycję skali.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

rysujemy wartość optymalną z niejasnego uniform prior w zakresie od -10 do 10(powinieneś zmienić ten prior, jeśli twoja postać jest poza tym zakresem). Ponieważ ten parametr może być dodatni lub ujemny, używamy przesunięcia slajdu, aby zaproponować zmiany podczas MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Model Ornsteina-Uhlenbecka

teraz, gdy określiliśmy parametry modelu, możemy wyciągnąć dane postaci z odpowiedniego filogenetycznego modelu OU. W tym przykładzie używamy algorytmu REMLA, aby skutecznie obliczyć prawdopodobieństwo (Felsenstein 1985). Zakładamy, że znak zaczyna się od optymalnej wartości u korzenia drzewa.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

zauważając, że $X$ jest obserwowanymi danymi (), zaciskamy data do tego węzła stochastycznego.

X.clamp(data)

na koniec tworzymy obiekt workspace dla całego modelu z model(). Pamiętaj, że obiekty workspace są inicjowane operatorem = i same nie są częścią bayesowskiego modelu graficznego. Funkcja model() przemierza cały wykres modelu i znajduje wszystkie węzły w określonym modelu. Obiekt ten zapewnia wygodny sposób odniesienia się do całego obiektu modelu, a nie tylko pojedynczego węzła DAG.

mymodel = model(theta)

uruchamianie analizy MCMC

określanie monitorów

aby przeprowadzić analizę MCMC, musimy ustawić wektor monitorów do rejestrowania Stanów naszego łańcucha Markowa. Wszystkie funkcje monitora są nazywane mn*, gdzie * jest symbolem wieloznacznym reprezentującym Typ monitora. Najpierw zainicjujemy monitor modelu za pomocą funkcji mnModel. Tworzy to nową zmienną monitora, która wyświetli Stany dla wszystkich parametrów modelu po przekazaniu do funkcji MCMC.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

dodatkowo Utwórz monitor ekranu, który będzie raportował Stany określonych zmiennych na ekranie za pomocą mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

inicjując i uruchamiając symulację MCMC

z w pełni określonym modelem, zestawem monitorów i zestawem ruchów, możemy teraz skonfigurować algorytm MCMC, który będzie pobierał wartości parametrów proporcjonalnie do ich tylnego prawdopodobieństwa. Funkcja mcmc() utworzy nasz obiekt MCMC:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

Teraz uruchom MCMC:

mymcmc.run(generations=50000)

po zakończeniu analizy będziesz miał monitorowane pliki w katalogu youroutput.

Rev plik do wykonania tej analizy: mcmc_OU.Rev

znaki rozwijające się w procesie OU mają tendencję do stacjonarnego rozkładu, który jest rozkładem normalnym ze średnią $\theta$ i wariancją $\sigma^2 \div 2\alpha$. Dlatego też, jeśli tempo ewolucji jest wysokie (lub gałęzie w drzewie są stosunkowo długie), może być trudno oszacować $\sigma^2$ I $\alpha$ oddzielnie, ponieważ obie określają długoterminową wariancję procesu. Możemy sprawdzić, czy wpływa to na naszą analizę, badając wspólny tylny rozkład parametrów W Tracer. Kiedy parametry są dodatnio skorelowane, powinniśmy wahać się interpretować ich rozkłady krańcowe (tzn. nie wnioskować osobno o szybkości adaptacji lub parametrze wariancji).

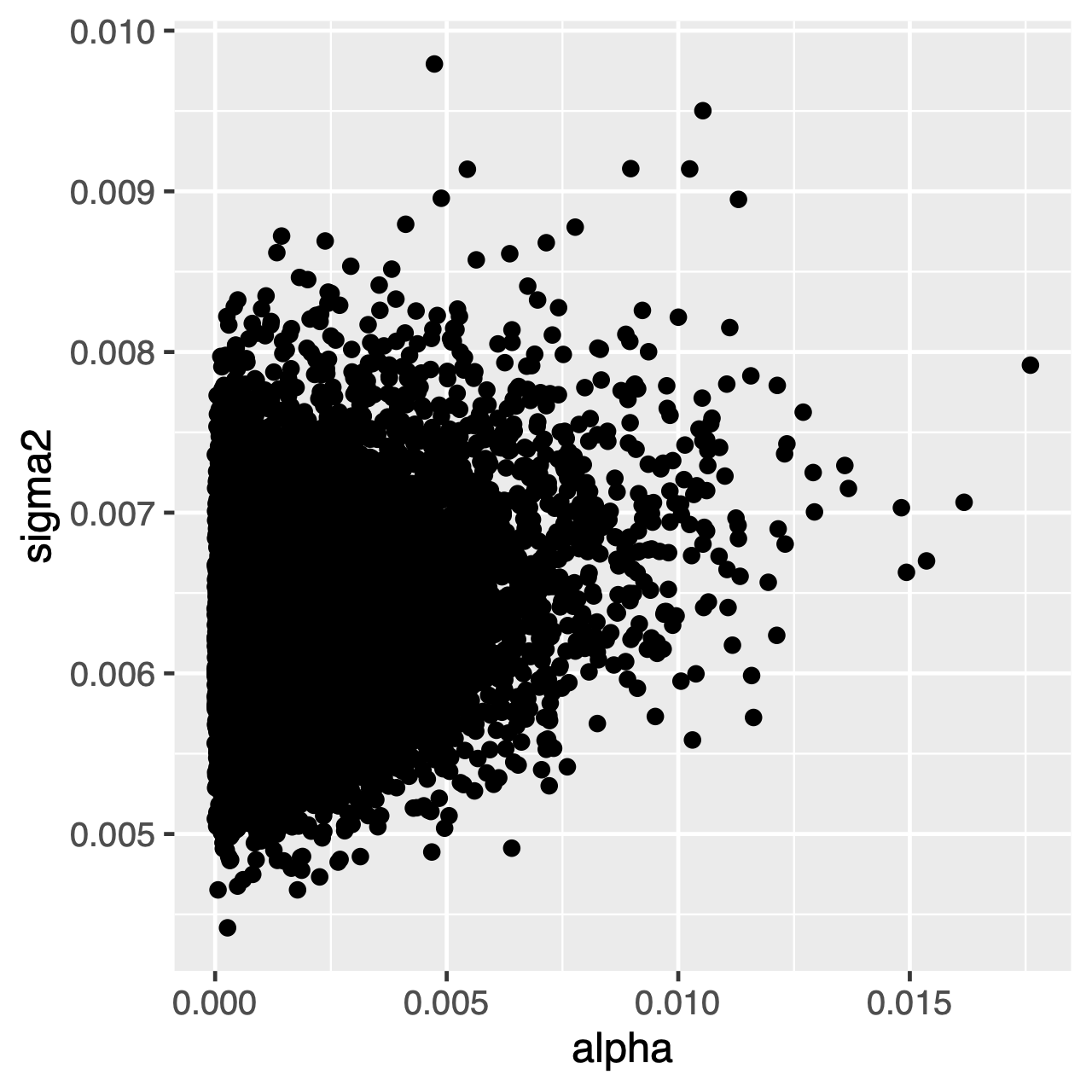
1

• Uruchom symulację MCMC w celu oszacowania tylnego rozkładu optimum OU (theta).
• załaduj wygenerowany plik wyjściowy do Tracer : jaka jest średnia Szacunkowa theta i jaka jest szacowana wartość HPD?
• użyj Tracer, aby porównać tylne rozkłady stawów alpha i sigma2. Czy te parametry są skorelowane czy nieskorelowane?
• Porównaj średnią przednią ze średnią tylną. (Podpowiedź: użyj opcjonalnego argumentu underPrior=TRUE w funkcji mymcmc.run()) czy są różne (np.)? Czy średnia tylna jest poza przedziałem prawdopodobieństwa 95%?

porównując modele OU i BM

teraz, gdy możemy dopasować zarówno modele BM, jak i OU, naturalnie możemy chcieć wiedzieć, który model pasuje lepiej. W tej sekcji dowiemy się, jak wykorzystać odwracalny skok Markova chain Monte Carlo do porównania dopasowania modeli OU i BM.

wybór modelu za pomocą odwracalnego Skoku MCMC

aby sprawdzić hipotezę, że postać ewoluuje w kierunku selektywnego optimum, wyobrażamy sobie dwa modele. Pierwszy model, w którym nie ma adaptacji do optimum, to przypadek, gdy $ \ alpha = 0$. Drugi model odpowiada modelowi OU z $ \ alpha > 0$. Działa to, ponieważ ruch Browna jest szczególnym przypadkiem modelu OU, gdy szybkość adaptacji wynosi 0. Niestety, ponieważ $ \ alpha$ jest parametrem ciągłym, standardowy łańcuch Markowa nigdy nie odwiedzi stanów, w których każda wartość jest dokładnie równa 0. Na szczęście możemy użyć odwracalnego skoku, aby umożliwić łańcuchowi Markowa rozważenie wizyty w modelu ruchu Browna. Wiąże się to z określeniem prawdopodobieństwa wstępnego dla każdego z dwóch modeli i dostarczeniem wcześniejszego rozkładu dla $\alpha$ dla modelu OU.

używanie rjMCMC pozwala łańcuchowi Markowa odwiedzić dwa modele proporcjonalnie do ich tylnego prawdopodobieństwa. Tylne prawdopodobieństwo modelu $i$ jest po prostu ułamkiem próbek, w których łańcuch odwiedzał ten model. Ponieważ w modelach określamy również prior, możemy obliczyć współczynnik Bayesa dla modelu OU jako:

\

gdzie $p (\text{OU model} \ mid X)$ i $p (\text{ou model})$ są odpowiednio prawdopodobieństwem tylnym i prawdopodobieństwem wstępnym modelu OU.

odwracalny skok między modelami OU i BM

aby włączyć rjMCMC, po prostu musimy umieścić odwracalny skok przed odpowiednim parametrem, $\alpha$. Możemy zmodyfikować poprzedni na alpha tak, że przyjmuje on stałą wartość 0 lub jest pobierany z poprzedniego rozkładu. Na koniec określamy prawdopodobieństwo wstępne dla modelu OU p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

następnie przedstawiamy propozycję odwracalnego skoku na alpha, która proponuje zmiany między tymi dwoma modelami.

moves.append( mvRJSwitch(alpha, weight=1.0) )

dodatkowo dostarczamy normalną propozycję mvScale, gdy MCMC odwiedza model OU.

moves.append( mvScale(alpha, weight=1.0) )

dołączamy zmienną, która ma wartość 1, gdy łańcuch odwiedza model OU, oraz odpowiednią zmienną, która ma wartość 1, gdy odwiedza model BM. Pozwoli nam to na Łatwe obliczenie tylnego prawdopodobieństwa modeli, ponieważ po prostu musimy obliczyć tylną średnią wartość tego parametru.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

ułamek próbek, dla których is_OU = 1 jest tylnym prawdopodobieństwem modelu OU. Alternatywnie, tylna średnia estymacja tej zmiennej wskaźnikowej odpowiada tylnemu prawdopodobieństwu modelu OU. Wartości te można wykorzystać w powyższym równaniu współczynnika Bayesa do obliczenia wsparcia współczynnika Bayesa dla każdego modelu.

1. Felsenstein J. 1985. Filogenies and the comparative method. Amerykański Przyrodnik.:1-15.10.1086/284325
2. Höhna S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. 2014. Probabilistyczna Graficzna reprezentacja modelu w Filogenetyce. Biologia Systematyczna. 63: 753-771.10.1093/sysbio/syu039
3. Landis M. J., Schraiber J. G. 2017. Pulsacyjna ewolucja ukształtowała współczesne rozmiary ciała kręgowców. Proceedings of the National Academy of Sciences. 114:13224-13229.10.1073/pnas.1710920114