Tensor Riemanna

Tensor Riemanna (Schutz 1985) , znany również jako Tensor krzywizny Riemanna-Christoffela (Weinberg 1972, s. 133; Arfken 1985, s. 123) lub Tensor krzywizny Riemanna (Misner et al. 1973, s. 218), jest tensorem czteropunktowym, który jest przydatny w ogólnej teorii względności. Inne ważne ogólne tensory relatywistyczne, takie jak tensor krzywizny Ricciego i krzywizna skalarna mogą być zdefiniowane w kategoriach .

Tensor Riemanna jest w pewnym sensie jedynym tensorem, który można skonstruować z tensora metrycznego i jego pierwszej i drugiej pochodnej,

(1)

gdziesą symbolami Christoffela pierwszego rodzaju,a jest pochodną przecinka (Schmutzer 1968, s. 108; Weinberg 1972). W jednym wymiarze, . W czterech wymiarach Znajduje się 256 elementów. Wykorzystanie relacji symetrii,

(2)

liczba niezależnych komponentów jest zmniejszona do 36. Korzystanie z warunku

(3)

liczba współrzędnych zmniejsza się do 21. Wreszcie, za pomocą

(4)

20 niezależne komponenty są pozostawione (Misner et al. 1973, s. 220-221;Arfken 1985, s. 123-124).

ogólnie liczba niezależnych elementów w wymiarach jest podana przez

(5)

„czterowymiarowe liczby piramidalne”, których pierwsze wartości to 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Liczba skalarów, które można skonstruować z i wynosi

(6)

(Weinberg 1972). Pierwsze kilka wartości to 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).

pod względem tensora Jacobiego ,

(7)

niech

(8)

gdzie ilość wewnątrz jest symbolem Christoffela drugiego rodzaju. Wtedy

(9)

rozbity na najprostszy rozkład w wymiarach,

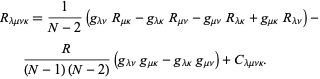(10)

tutaj jest tensorem krzywizny Ricciego, jest krzywizną skalarną, a jest tensorem Weyla.