pai de Família, Transformação
chefe de Família (Transformação também “chefe de Família de Reflexão”) é ortogonal a reflexão transformação:
- é reflexo de vetores em colunas da matriz tal que
- o primeiro vetor tem todos os zeros, exceto o primeiro elemento
A Matriz de Transformação
Reflexão transformação:
Propriedades de
chefe de Família matrizes são simétricas e ortogonal: eles são matrizes de reflexão
Derivação
Então temos $P = I – 2vv^T$:
utilizamos tais transformações para a anulação de elementos
Decomposição de QR
, Como no caso da Decomposição LU, onde aplicou-se uma série de Gauss Transformação alterações, nós podemos fazer o mesmo e executar uma série de chefe de Família Transformações
- então, se nós seleccione $y = \pm e_1$ (onde $e_1$ é a matriz com 1 na posição 1 e o descanso são zeros)
- em seguida, ele vai a zero todos os elementos de $x$, exceto o primeiro
- assim, através da escolha adequada de $H$ podemos tirar de $A$ e zero todas as sub-diagonal elementos
- pode fazer isso várias vezes para cada coluna de $A$
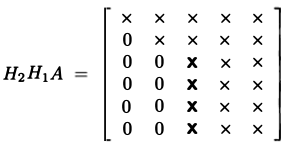
Desta forma, podemos realizar a Decomposição QR:
Hessenberg Decomposição
em Vez de usá-lo para reduzir a matriz Triangular, podemos usar pai de Família, de Transformação para reduzir uma matriz a Matriz de Hessenberg