Encontrar uma óptima solução para certos problemas de otimização pode ser incrivelmente difícil tarefa, muitas vezes, praticamente impossível. Isto porque, quando um problema se torna suficientemente grande, precisamos de procurar um enorme número de soluções possíveis para encontrar a solução ideal. Mesmo com o poder da computação moderna ainda existem muitas soluções possíveis para considerar. Neste caso, porque nós não podemos esperar realisticamente encontrar o ideal dentro de um período razoável de tempo, nós temos que nos contentar com algo que está perto o suficiente. Um exemplo de problema de otimização que normalmente tem um grande número de soluções possíveis seria o problema do vendedor ambulante. A fim de encontrar uma solução para um problema, como o problema do caixeiro viajante precisamos usar um algoritmo que é capaz de encontrar uma solução boa o suficiente em uma quantidade razoável de tempo. Em um tutorial anterior nós olhamos como nós poderíamos fazer isto com algoritmos genéticos, e embora algoritmos genéticos sejam uma maneira nós podemos encontrar uma solução ‘boa-suficiente’ para o problema do caixeiro viajante, há outros algoritmos mais simples que nós podemos implementar que também nos encontrarão uma solução próxima à solução ideal. Neste tutorial o algoritmo que vamos usar é, ‘simulado recozimento’.Se você não está familiarizado com o problema do caixeiro viajante, pode valer a pena dar uma olhada no meu tutorial anterior antes de continuar.O que é o recozimento simulado? em primeiro lugar, vamos olhar como funciona o recozimento simulado, e por que é bom em encontrar soluções para o problema do Caixeiro Viajante em particular. O algoritmo de recozimento simulado foi originalmente inspirado no processo de recozimento em metal. O recozimento envolve aquecimento e arrefecimento de um material para alterar as suas propriedades físicas devido às alterações na sua estrutura interna. À medida que o metal arrefece a sua nova estrutura torna-se fixo, fazendo com que o metal retenha as suas propriedades recentemente obtidas. Em recozimento simulado mantemos uma variável de temperatura para simular este processo de aquecimento. Inicialmente, ajustámo-lo alto e depois permitimos que arrefecesse lentamente à medida que o algoritmo corre. Embora esta variável de temperatura seja alta, o algoritmo será permitido, com mais frequência, aceitar soluções que são piores do que a nossa solução atual. Isso dá ao algoritmo a capacidade de saltar de qualquer otimismo local que se encontra no início da execução. À medida que a temperatura é reduzida, também é a chance de aceitar soluções piores, portanto, permitindo que o algoritmo se concentre gradualmente em uma área do espaço de busca em que esperamos, uma solução próxima de ótima pode ser encontrada. Este processo gradual de ‘resfriamento’ é o que faz com que o algoritmo de recozimento simulado seja notavelmente eficaz em encontrar uma solução próxima da ideal quando se lida com grandes problemas que contêm inúmeros otimums locais. A natureza do problema do vendedor ambulante torna-o um exemplo perfeito.Vantagens de recozimento simulado pode estar a pensar se há alguma vantagem real em implementar recozimento simulado sobre algo como um simples alpinista. Embora alpinistas podem ser surpreendentemente eficazes em encontrar uma boa solução, eles também têm uma tendência para ficar preso em otimums locais. Como nós determinamos anteriormente, o algoritmo de recozimento simulado é excelente para evitar este problema e é muito melhor em média para encontrar um ideal global aproximado.Para ajudar a compreender melhor, vamos ver rapidamente porque é que um algoritmo básico de escalada é tão propenso a ser apanhado em optimums locais.
um algoritmo alpinista simplesmente aceitará soluções vizinhas que são melhores do que a solução atual. Quando o alpinista não consegue encontrar vizinhos melhores, pára.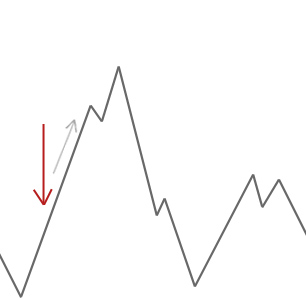
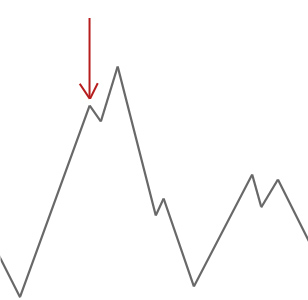
no exemplo acima começamos o nosso alpinista na seta vermelha e ele trabalha o seu caminho até chegar a um ponto onde não pode subir mais alto sem primeiro descer. Neste exemplo podemos ver claramente que está preso em um ótimo local. Se este fosse um problema do mundo real, não saberíamos como o espaço de busca parece, por isso, infelizmente, não seríamos capazes de dizer se esta solução está em algum lugar perto de um ideal global.
o recozimento simulado funciona de forma ligeiramente diferente e ocasionalmente aceitará soluções piores. Esta característica de recozimento simulado ajuda-o a saltar de qualquer otimum local que poderia ter ficado preso de outra forma.
função de aceitação
vamos dar uma olhada em como o algoritmo decide que soluções aceitar para que possamos entender melhor como é capaz de evitar estes optimums locais.Em primeiro lugar, verificamos se a solução vizinha é melhor do que a actual. Se for, aceitamos incondicionalmente. Se, no entanto, a solução vizinha não é melhor, precisamos considerar alguns fatores. Em primeiro lugar, quão pior é a solução vizinha; e, em segundo lugar, quão elevada é a actual “temperatura” do nosso sistema. A altas temperaturas, é mais provável que o sistema aceite soluções que são piores.
A matemática para isso é muito simples:
Basicamente, menor é a mudança na energia (a qualidade da solução), e quanto maior a temperatura, o mais provável é que o algoritmo para aceitar a solução.Como está o algoritmo? Bem, na sua implementação mais básica é bastante simples.
- primeiro precisamos definir a temperatura inicial e criar uma solução inicial aleatória.Então começamos a fazer looping até que a nossa condição de paragem seja cumprida. Normalmente, ou o sistema foi suficientemente arrefecido, ou foi encontrada uma solução suficientemente boa.
- a partir daqui selecionamos um vizinho, fazendo uma pequena mudança na nossa solução atual.
- então decidimos se vamos para essa solução vizinha.Finalmente, diminuímos a temperatura e continuamos a fazer looping .
inicialização da temperatura
para uma melhor otimização, ao inicializar a variável de temperatura devemos selecionar uma temperatura que permita inicialmente praticamente qualquer movimento contra a solução atual. Isso dá ao algoritmo a capacidade de explorar melhor todo o espaço de busca Antes de resfriar e se instalar em uma região mais focada.
código de exemplo
agora vamos usar o que sabemos para criar um algoritmo básico de recozimento simulado, e depois aplicá-lo ao problema do caixeiro viajante abaixo. Nós vamos usar Java neste tutorial, mas a lógica deve ser suficientemente simples para copiar para qualquer linguagem de sua escolha.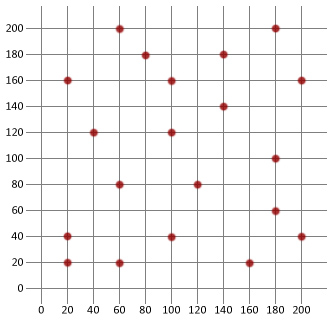
primeiro precisamos criar uma classe da cidade que pode ser usada para modelar os diferentes destinos de nosso vendedor ambulante.
City.java
* City.java
* Models a city
* /
package sa;
public class City {
int x;
int y;
// constrói uma cidade aleatoriamente colocada
cidade pública () {
isto.x = (int) (Math.random () * 200);
this.y = (int) (Math.Aleatório()*200);
}
// Constructs a city at chosen x, y location
public City (int x, int y){
this.x = x;
this.y = y;
}
// Gets city ‘ s x coordinate
public int getX () {
return this.x;
}
// Gets city’s y coordinate
public int getY(){
return this.y;
}
// Gets the distance to given city
public double distanceTo (City) {
int xDistance = Math.abs (getX) – city.getX ();
int yDistance = Math.abs (getY) – city.getY ();
double distance = Math.sqrt( (xDistance*xDistance) + (yDistance*yDistance) );
retornar à distância;
}
@Substituir
public String toString(){
retorno getX()+”, “+getY();
}
}
Seguinte, vamos criar uma classe que pode manter o controle das cidades.
TourManager.java
* TourManager.java
* Holds the cities of a tour
* /
package sa;
import java.util.Lista de matrizes;
>();
// adiciona uma cidade de destino a ‘public static void addCity’ (cidade da cidade) {
destinationCities.adicionar (cidade);
}
// Get a city
public static City getCity (int index){
return (City)destinationCities.get (índice);
}
// obter o número de cidades de destino
public static int number ofcities () {
return destinationCities.tamanho();
}
}
agora, para criar a classe que pode modelar uma viagem de vendedor.
Tour.java
* Tour.java
* armazena uma turnê candidata através de todas as cidades
*/
package sa;
import java.util.ArrayList;
importar java.util.Coleções;
public class Tour{
// Contém o nosso passeio de cidades
private ArrayList turnê = new ArrayList<Cidade>();
// Cache
private int distância = 0;
// Constrói um espaço em branco tour
Excursão pública(){
for (int i = 0; i < TourManager.number ofcities (); i++) {
tour.adicionar(null);
}
}
// Constructs a tour from another tour
public Tour (ArrayList tour){
this.tour = (ArrayList) tour.clone();
}
// Retorna informações sobre o passeio
public ArrayList getTour(){
retorno tour;
}
// Cria um aleatório individual
public void generateIndividual() {
// Loop através de todas as nossas cidades de destino e adicioná-los para o nosso tour
for (int cityIndex = 0; cityIndex < TourManager.number ofcities (); cityIndex++) {
setCity (cityIndex, TourManager.getCity(cityIndex));
}
// reordenar aleatoriamente a turnê
Collections.shuffle (tour);
/ Gets a city from the tour
public City getCity(int tourPosition) {
return (City)tour.get(posição do tour);
}
// coloca uma cidade em uma certa posição dentro de uma turnê.conjunto(tourPosition, cidade);
// Se os passeios foram alterados precisamos para repor a aptidão e a distância
distância = 0;
}
// Fica a distância total do passeio
public int getDistance(){
se (distância == 0) {
int tourDistance = 0;
// Loop através de nossa visita cidades
for (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Get cidade em que estamos viajando de
Cidade fromCity = getCity(cityIndex);
// Cidade em que estamos viajando para
Cidade destinationCity;
// Verifica nós não estamos na nossa turnê do último cidade, se formos definir o nosso
// passeio de final de cidade de destino para a nossa partida da cidade de
se(cityIndex+1 < tourSize()){
destinationCity = getCity(cityIndex+1);
}
else{
destinationCity = getCity(0);
}
// Obter a distância entre as duas cidades
tourDistance += fromCity.distanceTo (destinationCity);
}
distance = tourDistance;
}
distância de retorno;
}
// Conheça o número de cidades em nossa turnê
public int tourSize() {
return tour.tamanho();
}
@Substituir
public String toString() {
String geneString = “|”;
for (int i = 0; i < tourSize(); i++) {
geneString += getCity(eu)+”|”;
}
voltar geneString;
}
}
Finalmente, vamos criar nosso simulated annealing o algoritmo.
recozimento simulado.java
se (newEnergy < energia) {
retorno 1.0;
}
// se a nova solução for pior, calcule uma probabilidade de aceitação
return Math.exp((energy – newEnergy) / temperature);
}
public static void main(String args) {
/ Create and add our cities
City = new City (60, 200);
TourManager.addCity (cidade);
City2 = New City (180, 200);
TourManager.addCity(city2);
City city3 = new City (80, 180);
TourManager.city3;
City4 = Nova Cidade (140, 180);
TourManager.addCity(city4);
City city5 = new City (20, 160);
TourManager.city5; city6 = Nova Cidade (100, 160);
TourManager.cidade = Nova Cidade (200, 160);
TourManager.cidade nova(140, 140); Cidade Nova (8701).addCity (city8);
City city9 = new City(40, 120);
TourManager.addCity(city9);
City city10 = new City (100, 120);
TourManager.addCity (city10);
City city11 = new City(180, 100);
TourManager.addCity (city11);
City city12 = new City(60, 80);
TourManager.addCity (city12);
City city13 = new City(120, 80);
TourManager.addCity (city13);
City city14 = new City(180, 60);
TourManager.addCity (city14);
City city15 = new City(20, 40);
TourManager.addCity (city15);
City city16 = new City(100, 40);
TourManager.cidade = Nova Cidade (200, 40);
TourManager.addCity(city17);
City city18 = new City (20, 20);
TourManager.addCity (city18);
City city19 = new City(60, 20);
TourManager.addCity (city19);
City city20 = new City(160, 20);
TourManager.addCity (city20);
/ Set initial temp
double temp = 10000;
/ Cooling rate
double coolingRate = 0.003;
/ Initialize intial solution
Tour currentSolution = new Tour ();
currentSolution.generateIndividual (); sistema
.as.println (“inicial solution distance:” + currentSolution.getDistance ();
/ Set as current best
Tour best = new Tour (currentSolution.getTour ());
/ / Loop até que o sistema tenha arrefecido
while (temp > 1) {
// Create new neighbour tour
Tour newSolution = new Tour (currentSolution.getTour ();
// Get a random positions in the tour
int tourPos1 = (int) (newSolution.tourSize () * Math.random ();
int tourPos2 = (int) (newSolution.tourSize () * Math.random ();
// Get the cities at selected positions in the tour
City citySwap1 = newSolution.getCity (tourPos1);
City citySwap2 = newSolution.getCity (tourPos2);
/ Swap them
newSolution.setCity(tourPos2, citySwap1);
newSolution.setCity (tourPos1, citySwap2);
/ Get energy of solutions
int currentEnergy = currentSolution.getDistance ();
int vizinho = newSolution . getDistance ();
// Decide se devemos aceitar o vizinho
se (aceitabilidade (currentenergia, vizinho energia, temperatura) > Math.random ()) {
currentSolution = new Tour (newSolution.getTour());
}
// mantenha o controle da melhor solução encontrada
if (currentSolution.getdistance () < best.getdistance ()) {
best = new Tour (currentSolution.getTour());
}
// sistema de Arrefecimento
temperatura * = 1-taxa de arrefecimento;
}
sistema.as.println (“distância final da solução:” + melhor.getDistance (); sistema
.as.println(“Preço:” + melhor);
}
}
Saída
solução Final a distância: 911
Passeio: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
Conclusão
neste exemplo, nós fomos capazes de mais do que metade da distância de nossos inicial gerada aleatoriamente rota. Isto vai mostrar o quão útil este algoritmo relativamente simples é quando aplicado a certos tipos de problemas de otimização.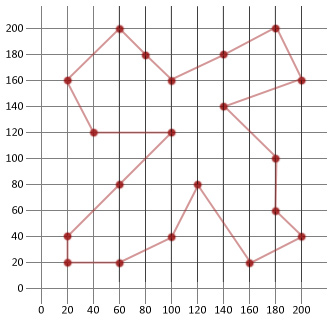
Author
 Hello, i’m Lee.Sou um desenvolvedor do Reino Unido que adora tecnologia e Negócios. Aqui você vai encontrar artigos e tutoriais sobre coisas que me interessam. Se me quiser contratar ou saber mais sobre mim, dirija-se à minha página
Hello, i’m Lee.Sou um desenvolvedor do Reino Unido que adora tecnologia e Negócios. Aqui você vai encontrar artigos e tutoriais sobre coisas que me interessam. Se me quiser contratar ou saber mais sobre mim, dirija-se à minha página