dacă ați citit postul anterior despre ceea ce este un inductor, să trecem la nivelul următor, ceea ce este circuitele formula inductanță.
acum că inductorul a fost adăugat la lista noastră de elemente pasive, este necesar să extindem instrumentul puternic de combinație serie-paralelă. Trebuie să știm cum să găsim inductanța echivalentă a unui set de inductoare conectate în serie sau conectate paralel găsite în circuitele practice.
seria Inductoare
luați în considerare o conexiune serie de n inductoare, așa cum se arată în figura.(1a), cu circuitul echivalent prezentat în figura.(1b).

inductoarele au același curent prin ele. Aplicând KVL la buclă,

înlocuirea Vk = LK di/dt are ca rezultat
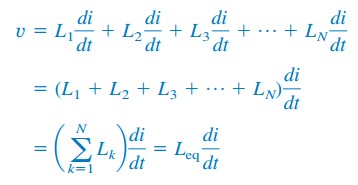
unde

astfel,
inductanța echivalentă a inductoarelor conectate în serie este suma inductanțelor individuale.
inductoarele în serie sunt combinate exact în același mod ca rezistențele în serie.
Inductoare paralele
considerăm acum o conexiune paralelă a n inductoare, așa cum se arată în figura.(2a), cu circuitul echivalent în figura.(2b). Inductoarele au aceeași tensiune peste ele. Folosind KCL,

dar


prin urmare,

unde
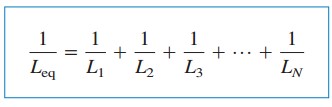
curentul inițial i (t0) prin Leq la t= t0 este de așteptat de KCL să fie suma curenților inductori la t0. Astfel, conform ecuației.(5),
![]()
conform ecuației.(6),
inductanța echivalentă a inductoarelor paralele este reciproca sumei reciprocelor inductanțelor individuale.
rețineți că inductoarele în paralel sunt combinate în același mod ca rezistențele în paralel.
pentru doi inductori în paralel (N = 2), ecuație.(6) devine
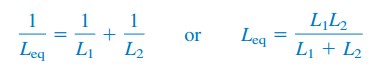
Exemple de circuite cu Formula inductanței
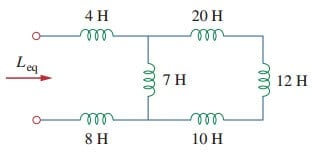
1. Găsiți inductanța echivalentă a circuitului prezentat în figura.(3).
soluție:
inductoarele 10-H, 12-H și 20-H sunt în serie; astfel, combinarea lor dă o inductanță de 42-H. Acest inductor 42-H este în paralel cu inductorul 7-H, astfel încât acestea să fie combinate, pentru a da


acest inductor 6-H este în serie cu inductoarele 4-H și 8-H. Prin Urmare,
![]()
2. Pentru circuitul din Figura.(4),
i(t) = 4(2 − e−10t) mA. Dacă i2(0) = -1 mA, găsiți:
(a) i1(0);
(b) v(t), v1(t) și v2(t);
(c) i1(t) și i2(t).

soluție:
(a) de la i (t) = 4 (2−e-10t) mA, i(0) = 4(2 − 1) = 4 mamă.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(c) curentul I1 este obținut ca


în mod similar,


rețineți că i1(t) + i2(t) = i(t).