modele simple Ornstein-Uhlenbeck

estimarea optima evolutivă

acest tutorial demonstrează cum se specifică un model Ornstein-Uhlenbeck în care se presupune că fenotipul optim este constant între ramurile unei filogenii calibrate în timp (referință lipsă) folosind seturile de date ale (jurnal) dimensiunea corpului peste clade vertebrate din (referință lipsă). Oferim reprezentarea probabilistică a modelului grafic al fiecărei componente pentru acest tutorial. După specificarea modelului, veți estima parametrii evoluției Ornstein-Uhlenbeck folosind lanțul Markov Monte Carlo (MCMC).

Ornstein-Uhlenbeck Model

sub modelul simplu Ornstein-Uhlenbeck (OU), se presupune că un caracter continuu evoluează spre o valoare optimă, $\theta$. Caracterul evoluează stocastic în funcție de un parametru de drift, $\sigma^2$. Caracterul este tras spre optim prin rata de adaptare, $ \ alpha$; valorile mai mari ale alfa indică faptul că personajul este tras mai puternic spre $\theta$. Pe măsură ce personajul se îndepărtează de $\theta$, parametrul $\alpha$ determină cât de puternic este tras Caracterul înapoi. Din acest motiv, $\alpha$ este uneori denumit parametru „bandă de cauciuc”. Când rata parametrului de adaptare $ \ alpha = 0$, modelul OU se prăbușește la modelul BM. Modelul grafic rezultat este destul de simplu, deoarece probabilitatea caracterelor continue depinde doar de filogenie (pe care presupunem că o cunoaștem în acest tutorial) și de parametrul trei OU ().

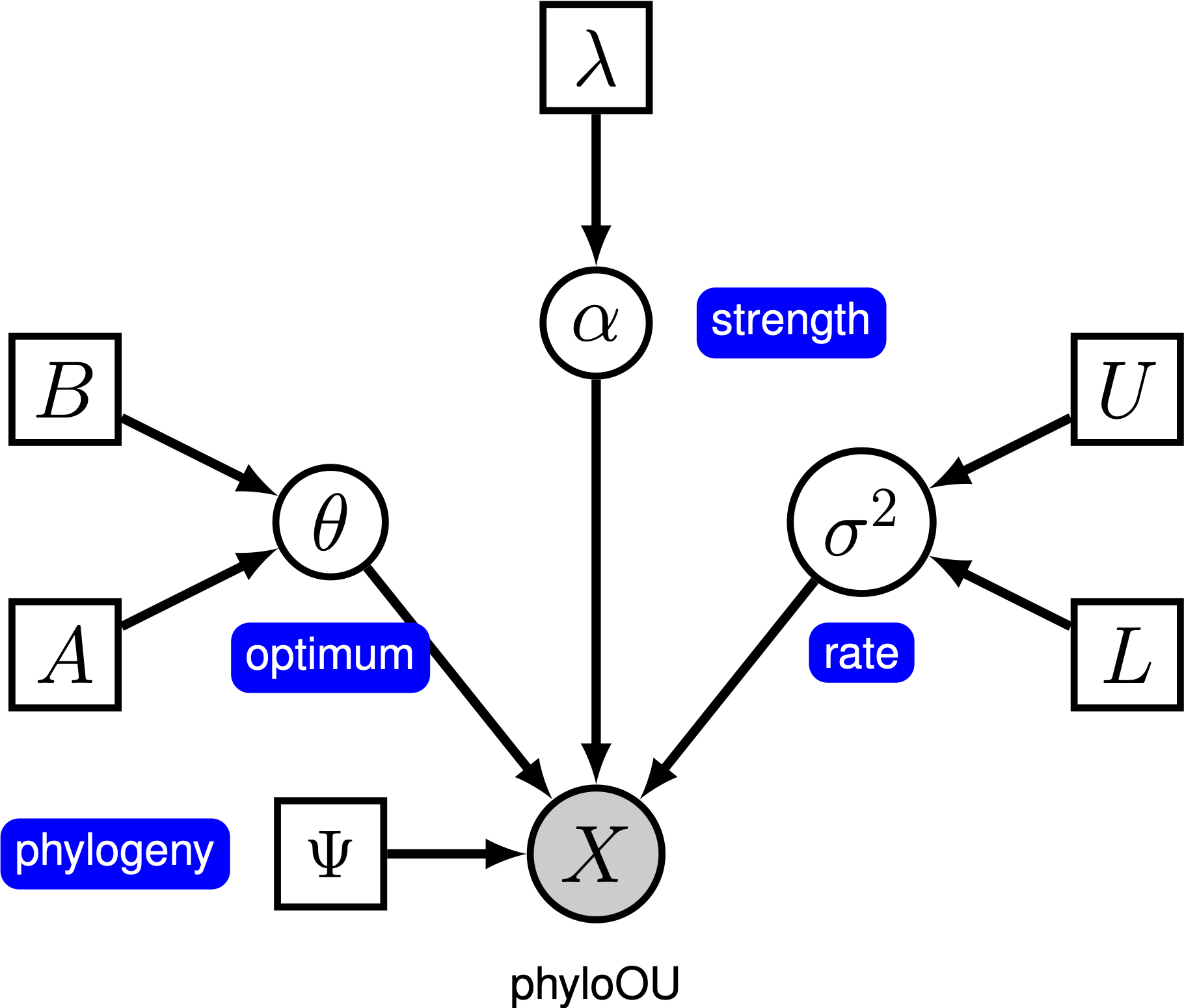
în acest tutorial, folosim cele 66 de filogenii vertebrate și seturi de date (log) pentru dimensiunea corpului din (Landis and Schraiber 2017).

XV specificația completă a modelului OU se află în fișierul numit mcmc_OU.Rev.

Citiți datele

începem prin a decide care dintre cele 66 de seturi de date vertebrate să le folosim. Aici, presupunem că analizăm primul set de date (Acanthuridae), dar ar trebui să nu ezitați să alegeți oricare dintre seturile de date.

dataset <- 1

acum, citim în arborele (calibrat în timp) corespunzător setului de date ales.

T <- readTrees("data/trees.nex")

apoi, citim în datele caracterelor pentru același set de date.

data <- readContinuousCharacterData("data/traits.nex")

în plus, inițializăm o variabilă pentru vectorul nostru de mișcări și monitoare:

moves = VectorMoves()monitors = VectorMonitors()

specificând modelul

Model Arbore

în acest tutorial, presupunem că arborele este cunoscut fără zonă. Creăm un nod constant pentru copac care corespunde filogeniei observate.

tree <- T

parametrul ratei

rata stocastică de evoluție este controlată de parametrul ratei, $\sigma^2$. Tragem parametrul ratei dintr-un prior loguniform. Acest prior este uniform pe scara jurnalului, ceea ce înseamnă că reprezintă ignoranța cu privire la ordinea de mărime a ratei.

sigma2 ~ dnLoguniform(1e-3, 1)

pentru a estima distribuția posterioară a $ \ sigma^2$, trebuie să oferim un mecanism de propunere MCMC care funcționează pe acest nod. Deoarece $ \ sigma^2$ este un parametru de rată și, prin urmare, trebuie să fie pozitiv, folosim o mișcare de scalare numită mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

parametrul de adaptare

rata de adaptare la optim este determinată de parametrul $\alpha$. Atragem $ \ alpha$ dintr-o distribuție anterioară exponențială și plasăm o propunere de scară pe ea.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

extragem valoarea optimă dintr-un prior uniform vag cuprins între -10 și 10 (ar trebui să schimbați acest prior dacă caracterul dvs. este în afara acestui interval). Deoarece acest parametru poate fi pozitiv sau negativ, folosim o mișcare de diapozitive pentru a propune modificări în timpul MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Modelul Ornstein-Uhlenbeck

acum că am specificat parametrii modelului, putem extrage datele caracterelor din modelul filogenetic OU corespunzător. În acest exemplu, folosim algoritmul REML pentru a calcula eficient probabilitatea (Felsenstein 1985). Presupunem că caracterul începe la valoarea optimă la rădăcina copacului.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

observând că $X$ este datele observate (), fixăm data la acest nod stochastic.

X.clamp(data)

în cele din urmă, vom crea un obiect spațiu de lucru pentru întregul model cu model(). Amintiți-vă că obiectele spațiului de lucru sunt inițializate cu operatorul = și nu fac ele însele parte din modelul grafic Bayesian. Funcția model() traversează întregul grafic model și găsește toate nodurile din modelul pe care l-am specificat. Acest obiect oferă o modalitate convenabilă de a se referi la întregul obiect model, mai degrabă decât la un singur nod DAG.

mymodel = model(theta)

rularea unei analize MCMC

specificarea monitoarelor

pentru analiza noastră MCMC, trebuie să configurăm un vector de monitoare pentru a înregistra stările lanțului nostru Markov. Funcțiile monitorului se numesc mn*, unde * este wildcard-ul care reprezintă tipul monitorului. În primul rând, vom inițializa monitorul modelului folosind funcția mnModel. Aceasta creează o nouă variabilă de monitor care va afișa stările pentru toți parametrii modelului atunci când este trecută într-o funcție MCMC.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

în plus, creați un monitor de ecran care va raporta stările variabilelor specificate pe ecran cu mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

inițializarea și rularea simulării MCMC

cu un model complet specificat, un set de monitoare și un set de mișcări, acum putem configura algoritmul MCMC care va proba valorile parametrilor înproporție la probabilitatea lor posterioară. Funcția mcmc() va crea obiectul nostru MCMC:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

acum, rulați MCMC:

mymcmc.run(generations=50000)

când analiza este completă, veți avea fișierele monitorizate în directorul youroutput.

XV fișierul Rev pentru efectuarea acestei analize: mcmc_OU.Rev

caracterele care evoluează în cadrul procesului OU vor tinde spre o distribuție staționară, care este o distribuție normală cu media $\theta$ și varianța $\sigma^2 \div 2\alpha$. Prin urmare, dacă ratele de evoluție sunt ridicate (sau ramurile din copac sunt relativ lungi), poate fi dificil să se estimeze separat $\sigma^2$ și $\alpha$, deoarece ambele determină varianța pe termen lung a procesului. Putem vedea dacă acest lucru afectează analiza noastră prin examinarea distribuției posterioare comune a parametrilor în Tracer. Când parametrii sunt corelați pozitiv, ar trebui să ezităm să interpretăm distribuțiile lor marginale (adică să nu facem inferențe despre rata de adaptare sau parametrul de varianță separat).

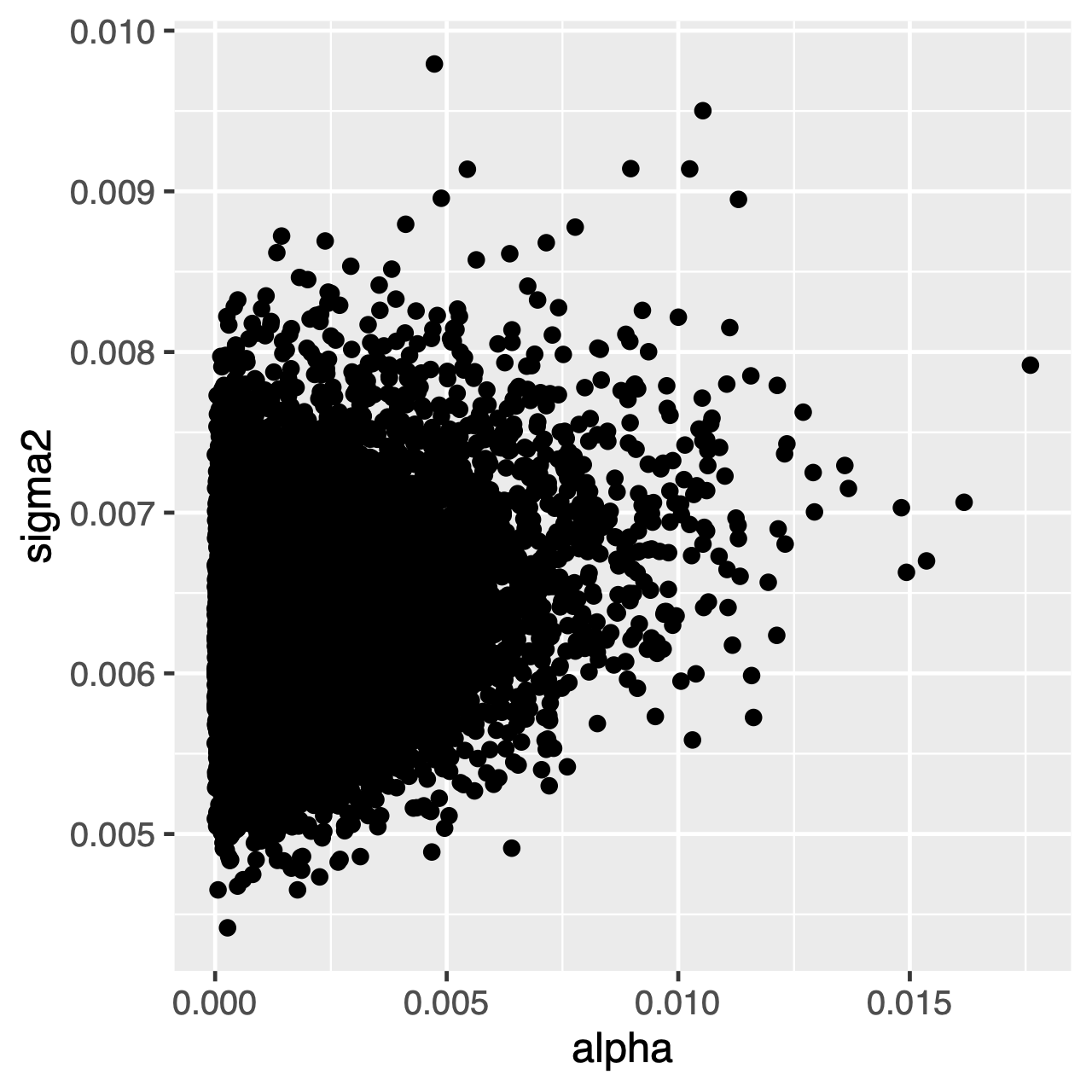
exercițiu 1

• rulați o simulare MCMC pentru a estima distribuția posterioară a optimului OU (theta).
• încărcați fișierul de ieșire generat în Tracer: care este estimarea medie posterioară a theta și care este HPD estimat?
• utilizați Tracer pentru a compara distribuțiile posterioare comune ale alpha și sigma2. Sunt acești parametri corelați sau necorelați?
• comparați media anterioară cu media posterioară. (Sugestie :utilizați argumentul opțional underPrior=TRUE în funcția mymcmc.run()) sunt diferite (de exemplu,)? Este media posterioară în afara intervalului anterior de probabilitate de 95%?

comparând modelele OU și BM

acum, că putem potrivi atât modelele BM, cât și OU, am putea dori în mod natural să știm ce model se potrivește mai bine. În această secțiune, vom învăța cum să folosim lanțul reversibil-jump Markov Monte Carlo pentru a compara potrivirea modelelor OU și BM.

selectarea modelului folosind reversibil-Salt MCMC

pentru a testa ipoteza că un caracter evoluează spre un optim selectiv, ne imaginăm două modele. Primul model, în care nu există o adaptare la optim, este cazul când $\alpha = 0$. Al doilea model corespunde modelului OU cu $\alpha > 0$. Acest lucru funcționează deoarece mișcarea browniană este un caz special al modelului OU atunci când rata de adaptare este 0. Din păcate, deoarece $ \ alpha$ este un parametru continuu, un lanț Markov standard nu va vizita niciodată state în care fiecare valoare este exact egală cu 0. Din fericire, putem folosi salt reversibil pentru a permite lanțului Markov să ia în considerare vizitarea modelului Brownian-motion. Aceasta implică specificarea probabilității anterioare pe fiecare dintre cele două modele și furnizarea distribuției anterioare pentru $\alpha$ pentru modelul OU.

utilizarea rjMCMC permite lanțului Markov să viziteze cele două modele proporțional cu probabilitatea lor posterioară. Probabilitatea posterioară a modelului $i$ este pur și simplu fracțiunea de eșantioane în care lanțul vizita acel model. Deoarece specificăm și un prior pe modele, putem calcula un factor Bayes pentru modelul OU ca:

\

unde $P( \text{OU model} \mid X)$ și $p( \text{OU model})$ sunt probabilitatea posterioară și, respectiv, probabilitatea anterioară a modelului OU.

reversibil-salt între modelele OU și BM

pentru a activa rjMCMC, trebuie pur și simplu să plasăm un salt reversibil înainte pe parametrul relevant, $\alpha$. Putem modifica priorul pe alpha astfel încât să ia fie o valoare constantă de 0, fie să fie extrasă dintr-o distribuție anterioară. În cele din urmă, specificăm o probabilitate anterioară pe modelul OU de p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

apoi oferim o propunere reversibilă pe alpha care propune schimbări între cele două modele.

moves.append( mvRJSwitch(alpha, weight=1.0) )

în plus, oferim propunerea normală mvScale pentru momentul în care MCMC vizitează modelul OU.

moves.append( mvScale(alpha, weight=1.0) )

includem o variabilă care are o valoare 1 când lanțul vizitează modelul OU și o variabilă corespunzătoare care are o valoare 1 când vizitează modelul BM. Acest lucru ne va permite să calculăm cu ușurință probabilitatea posterioară a modelelor, deoarece pur și simplu trebuie să calculăm valoarea medie posterioară a acestui parametru.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

fracția de probe pentru care is_OU = 1 este probabilitatea posterioară a modelului OU. Alternativ, estimarea medie posterioară a acestei variabile indicatoare corespunde probabilității posterioare a modelului OU. Aceste valori pot fi utilizate în ecuația factorului Bayes de mai sus pentru a calcula suportul factorului Bayes pentru oricare dintre modele.

1. Felsenstein J. 1985. Filogeniile și metoda comparativă. Naturalistul American.:1-15.10.1086/284325
2. H Oktoshna S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. 2014. Reprezentarea probabilistică a modelului grafic în filogenetică. Biologie Sistematică. 63: 753-771.10.1093/sysbio/syu039
3. Landis M. J., Schraiber J. G. 2017. Evoluția pulsată a modelat dimensiunile moderne ale corpului vertebratelor. Lucrările Academiei Naționale de științe. 114: 13224-13229.10. 1073 / pnas.1710920114