Riemann Tensor

tensorul Riemann (Schutz 1985) , cunoscut și tensorul de curbură Riemann-Christoffel (Weinberg 1972, p. 133; arfken 1985, p. 123) sau tensorul de curbură Riemann (Misner și colab. 1973, p.218), este un tensor cu patru indici care este util în relativitatea generală. Alți tensori relativiști generali importanți, astfel încât tensorul de curbură Ricci și curbura scalară pot fi definite în termeni de .

tensorul Riemann este într-un anumit sens singurul tensor care poate fi construit din tensorul metric și primul și al doilea derivat al acestuia,

(1)

unde sunt simboluri Christoffel de primul fel și este un derivat de virgulă (Schmutzer 1968, p. 108; Weinberg 1972). Într-o singură dimensiune, . În patru dimensiuni, există 256 de componente. Utilizarea relațiilor de simetrie,

(2)

Numărul de componente independente este redus la 36. Utilizarea condiției

(3)

Numărul de coordonate se reduce la 21. În cele din urmă, folosind

(4)

20 componentele independente sunt lăsate (Misner și colab. 1973, pp.220-221;Arfken 1985, pp. 123-124).

în general, numărul de componente independente în dimensiuni este dat de

(5)

„numerele piramidale în patru dimensiuni”, primele valori ale cărora sunt 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Numărul de scalari care pot fi construiți din și este

(6)

(Weinberg 1972). Primele valori sunt apoi 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).

în ceea ce privește tensorul Jacobi ,

(7)

să

(8)

unde cantitatea din interiorul este un simbol Christoffel de al doilea tip. Atunci

(9)

defalcat în cea mai simplă descompunere în dimensiuni,

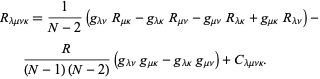(10)

aici, este tensorul de curbură Ricci, este curbura scalară și este tensorul Weyl.