He comenzado a hacer el popular curso de aprendizaje automático de Andrew Ng en Coursera. La primera semana cubre mucho, al menos para alguien que no ha tocado mucho cálculo durante unos años
- Funciones de costo (diferencia de medias al cuadrado)
- Descenso de gradiente
- Regresión lineal
Estos tres temas eran mucho para asimilar. Hablaré de cada uno en detalle, y de cómo encajan todos juntos, con un poco de código python para demostrar.
Editar 4 de mayo: Publiqué un seguimiento centrado en cómo funciona la función de Costo aquí, incluida una intuición, cómo calcularla a mano y dos implementaciones de Python diferentes. Puedo hacer un descenso de gradiente y luego unirlos para una regresión lineal pronto.
Representación de modelos
En primer lugar, el objetivo de la mayoría de los algoritmos de aprendizaje automático es construir un modelo: una hipótesis que se puede usar para estimar Y en función de X. La hipótesis, o modelo, asigna entradas a salidas. Por ejemplo, digamos que entreno un modelo basado en un montón de datos de vivienda que incluyen el tamaño de la casa y el precio de venta. Al entrenar a un modelo, puedo darle una estimación de cuánto puede vender su casa en función de su tamaño. Este es un ejemplo de un problema de regresión: dado algo de entrada, queremos predecir una salida continua.
La hipótesis que se presenta generalmente como

theta valores de los parámetros.
Algunos ejemplos rápidos de cómo visualizamos la hipótesis de:
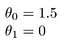
Esto produce que h(x) = 1.5 + 0x. 0x significa que no hay pendiente, y siempre será la constante 1.5. Esto se parece a:

¿
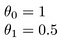

El objetivo de la creación de un modelo es elegir los parámetros o valores de theta, de modo que h(x) está cerca y para los datos de entrenamiento, de x y de y. Así que para estos datos
x =
y =

Intentaré encontrar una línea de mejor ajuste usando regresión lineal. Empecemos.
Función de coste
Necesitamos una función que minimice los parámetros de nuestro conjunto de datos. Una función común que se usa a menudo es el error cuadrado medio, que mide la diferencia entre el estimador (el conjunto de datos) y el valor estimado (la predicción). Se parece a esto:

Resulta que podemos ajustar un poco la ecuación para hacer el cálculo un poco más simple. Terminamos con:
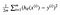
Vamos a aplicar este const función a la siga de datos:

Por ahora vamos a calcular algunos valores de theta, y grafique la función de costo por mano. Dado que esta función pasa a través de (0, 0), solo estamos viendo un solo valor de theta. De aquí en adelante, me referiré a la función de costo como J (Θ).
Para J (1), obtenemos 0. No es de extrañar: un valor de J (1) produce una línea recta que se ajusta perfectamente a los datos. ¿Qué tal J (0,5)?

El MSE función nos da un valor de 0.58. Vamos a la trama tanto de nuestros valores hasta ahora:
J(1) = 0
J(0.5) = 0.58

voy a seguir adelante y calcular algunos más de los valores de J(Θ).

Y si unimos los puntos muy bien juntos…

podemos ver que la función de costo es mínimo cuando theta = 1. Esto tiene sentido: nuestros datos iniciales son una línea recta con una pendiente de 1 (la línea naranja de la figura anterior).
Descenso de gradiente
Minimizamos J (Θ) por ensayo y error anterior, simplemente probando muchos valores e inspeccionando visualmente el gráfico resultante. ¿Debe haber una manera mejor? Descenso de gradiente de cola. El descenso de gradiente es una función general para minimizar una función, en este caso la función de costo de Error Cuadrado Medio.
El descenso de gradiente básicamente solo hace lo que estábamos haciendo a mano: cambiar los valores o parámetros theta, poco a poco, hasta que esperemos que lleguemos a un mínimo.
Comenzamos inicializando theta0 y theta1 a dos valores cualesquiera, digamos 0 para ambos, y pasamos de allí. Formalmente, el algoritmo es el siguiente:

donde α, alfa, es la tasa de aprendizaje, o la rapidez con la que queremos avanzar hacia el mínimo. Sin embargo, si α es demasiado grande, podemos rebasar.

Traer todo junto — Regresión Lineal
Rápidamente resumiendo:
Tenemos una hipótesis:

que necesitamos ajuste a nuestros datos de entrenamiento. Podemos usar una función de costo como Error cuadrado Medio:

que podemos minimizar usando descenso de gradiente:

Lo que nos lleva a nuestro primer algoritmo de aprendizaje automático, la regresión lineal. La última pieza del rompecabezas que necesitamos resolver para tener un modelo de regresión lineal en funcionamiento es el derivado parcial de la función de costo:
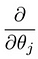
Que resulta ser:
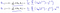
Que nos da de regresión lineal!
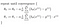
Con la teoría de la forma, me voy a poner en práctica esta lógica en python en el próximo post.
Editar 4 de mayo: Publiqué un seguimiento centrado en cómo funciona la Función de Costo aquí, incluida una intuición, cómo calcularla a mano y dos implementaciones de Python diferentes. Puedo hacer un descenso de gradiente y luego unirlos para una regresión lineal pronto.