Riemann Tensor

Riemann tensor (1985) , også kendt Riemann-Christoffel curvature tensor (1972, s. 133; Arfken 1985, s. 123) eller Riemann curvature tensor (Misner et al. 1973, s.218), er en fire-indeks tensor, der er nyttig i generel relativitet. Andre vigtige generelle relativistiske tensorer, således at Ricci curvature tensor og scalar curvature kan defineres i form af .

Riemann tensor er i en vis forstand den eneste tensor, der kan konstrueres fraden metriske tensor og dens første og anden derivater,

(1)

hvor er Christoffel symboler af den første slags og er et kommaderivat (Schmutser 1968, s. 108; Veinberg 1972). I en dimension, . I fire dimensioner er der 256 komponenter. Brug af symmetri-relationerne,

(2)

antallet af uafhængige komponenter reduceres til 36. Brug af tilstanden

(3)

antallet af koordinater reduceres til 21. Endelig ved hjælp af

(4)

20 uafhængige komponenter er tilbage (Misner et al. 1973, s.220-221;Arfken 1985, s. 123-124).

generelt er antallet af uafhængige komponenter i dimensioner givet af

(5)

de “fire-dimensionelle pyramidale tal”, hvoraf de første få værdier er 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Antallet af skalarer, der kan konstrueres fra og er

(6)

(1972). De første få værdier er derefter 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).

i form af Jacobi tensor ,

(7)

lad

(8)

hvor mængden inde i er et Christoffel symbol af den anden slags. Derefter

(9)

opdelt i sin enkleste nedbrydning i dimensioner,

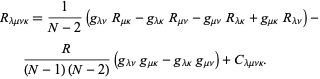(10)

her er Ricci curvature tensor, er den skalære krumning, og er Veyl tensor.