Der ELISA-Assay liefert drei verschiedene Arten der Datenausgabe:
Quantitativ
ELISA-Daten können im Vergleich zu einer Standardkurve (einer seriellen Verdünnung eines bekannten, gereinigten Antigens) interpretiert werden, um die Antigenkonzentrationen in verschiedenen Proben genau zu berechnen (Abbildung 6).
ELISAs können auch verwendet werden, um eine Ja- oder Nein-Antwort zu erhalten, die angibt, ob ein bestimmtes Antigen in einer Probe vorhanden ist, verglichen mit einer leeren Vertiefung, die kein Antigen oder ein nicht verwandtes Kontrollantigen enthält.
Semi-quantitativ
ELISAs können verwendet werden, um die relativen Antigenspiegel in Assayproben zu vergleichen, da die Intensität des Signals direkt mit der Antigenkonzentration variiert.
Standardkurve
ELISA-Daten werden typischerweise mit optischer Dichte vs. Log-Konzentration grafisch dargestellt, um eine Sigmoidkurve zu erzeugen, wie in Abbildung 6 gezeigt. Bekannte Konzentrationen des Antigens werden verwendet, um eine Standardkurve zu erzeugen, und dann werden diese Daten verwendet, um die Konzentration unbekannter Proben durch Vergleich mit dem linearen Teil der Standardkurve zu messen. Dies kann direkt in der Grafik oder mit einer Kurvenanpassungssoftware erfolgen, die normalerweise bei ELISA-Plattenlesern zu finden ist.
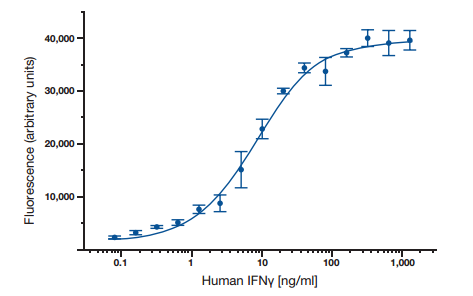
Abb. 6. Eine typische ELISA-Standardkurve.
Kalibrierkurvenmodelle
Wenn ein quantitatives Ergebnis benötigt wird, ist es am einfachsten, das Dreifache der Standardwerte zu mitteln und den Messwert der leeren Kontrollprobe abzuziehen. Zeichnen Sie als Nächstes die Standardkurve, suchen Sie die Linie der besten Anpassung oder zeichnen Sie zumindest eine Punkt-zu-Punkt-Kurve, damit die Konzentration der Proben bestimmt werden kann. Alle Verdünnungen müssen in diesem Stadium angepasst werden. Dies ist im Allgemeinen der praktische Umfang, in dem manuelle Berechnungen durchgeführt werden können.
Eine Variante besteht darin, die Daten mit Semi-Log, log / log, log / logit und seinen Ableitungen zu zeichnen – den logistischen Modellen mit 4 oder 5 Parametern. Die Verwendung softwarebasierter / automatisierter Lösungen ermöglicht es, anspruchsvollere grafische Ansätze in Betracht zu ziehen. Die Verwendung der linearen Regression innerhalb eines Softwarepakets fügt mehrere weitere Überprüfungsmöglichkeiten hinzu; Es ist möglich, den R2-Wert zu überprüfen, um die Gesamtanpassungsgüte zu bestimmen. Für den Teil der Kurve, in dem das Verhältnis von Konzentration zu Anzeige eine lineare Beziehung aufweist, stellen R2-Werte > 0,99 eine sehr gute Anpassung dar. Die Genauigkeit kann dann durch Verwendung weiterer Standardkonzentrationen in diesem Bereich weiter verbessert werden.
Ein Aspekt des linearen Diagramms besteht darin, dass die Datenpunkte auf den unteren Konzentrationen der Standardkurve komprimiert werden, wodurch dieser Bereich am genauesten ist (Bereich, in dem der erforderliche R2-Wert am wahrscheinlichsten erreicht wird). Um dieser Komprimierung entgegenzuwirken, kann ein Semi-Log-Diagramm verwendet werden; Hier wird das Log des Konzentrationswerts (auf der x-Achse) gegen die Anzeige (auf der y-Achse) aufgetragen. Diese Methode ergibt eine S-förmige Datenkurve, die mehr Datenpunkte in das benutzerfreundlichere Sigmoidmuster verteilt.
Der Diagrammtyp log / log (Konzentrationsprotokoll gegen Ausleseprotokoll) schafft es, mehr von der Datenkurve zu linearisieren. Der niedrige bis mittlere Standardkonzentrationsbereich ist in diesem Modell im Allgemeinen linear, nur das höhere Ende des Bereichs neigt dazu, abzufallen. Das log / logit und seine Ableitungen, die logistischen Modelle mit 4 oder 5 Parametern, sind anspruchsvoller und erfordern komplexere Berechnungen und Schätzungen von Max-, Min-, EC50- und Steigungswerten. Das 5-Parameter-Modell benötigt zusätzlich den Asymmetriewert.
Während diese Kalibrationskurvenmodelle eine verbesserte Leistung liefern können, wäre ein guter Ausgangspunkt die Verwendung des Log-Log-Diagramms mit einer Überprüfung des Wiederherstellungsprozentsatzes (Analytrückgewinnung aus gespickten Proben). Alternativ ist zumindest eine Rückanpassung der Standardkurvenauslesewerte häufig ein ausreichend guter Ansatz. Der einfachste Weg, dies zu überprüfen, besteht darin, die Kalibrierstandards zurück zu berechnen und zu überprüfen, ob sie innerhalb von 20% des Nennwerts der Anzeige liegen. Eine Einschränkung besteht darin, sich nicht auf ‚gute‘ R2-Werte zu verlassen und das Kalibrierkurvenmodell zu finden, das die besten Wiederherstellungswerte für die Standards liefert.
ELISA-Empfindlichkeit
ELISAs sind einer der empfindlichsten verfügbaren Immunoassays. Der typische Nachweisbereich für einen ELISA beträgt 0,1 bis 1 fmol oder 0,01 ng bis 0,1 ng, wobei die Empfindlichkeit von den besonderen Eigenschaften der Antikörper-Antigen-Wechselwirkung abhängt. Darüber hinaus können einige Substrate, wie z. B. solche, die ein verbessertes chemilumineszierendes oder fluoreszierendes Signal liefern, verwendet werden, um die Ergebnisse zu verbessern.
Wie bereits erwähnt, erzeugt die indirekte Erkennung höhere Signalpegel und sollte daher empfindlicher sein. Es kann jedoch auch ein höheres Hintergrundsignal verursachen, wodurch die spezifischen Nettosignalpegel reduziert werden.