Der Riemann-Tensor (Schutz 1985) 
, auch bekannt als Riemann-Christoffel-Krümmungstensor (Weinberg 1972, S. 133; Arfken 1985, S. 123) oder Riemann-Krümmungstensor (Misner et al. 1973, S. 218), ist ein Vier-Index-Tensor, der in der allgemeinen Relativitätstheorie nützlich ist. Andere wichtige allgemeine relativistische Tensoren, so dass der Ricci-Krümmungstensor und die Skalarkrümmung in Bezug auf 
definiert werden können.
Der Riemann-Tensor ist in gewissem Sinne der einzige Tensor, der aus dem metrischen Tensor und seiner ersten und zweiten Ableitung konstruiert werden kann,
 |
(1)
|
wobei 
Christoffel-Symbole der ersten Art sind und 
eine Komma-Ableitung ist (Schmutzer 1968, S. 108; Weinberg 1972). In einer Dimension ist 
. In vier Dimensionen gibt es 256 Komponenten. Nutzung der Symmetriebeziehungen,
 |
(2)
|
die Anzahl der unabhängigen Komponenten wird auf 36 reduziert. Verwenden der Bedingung
 |
(3)
|
die Anzahl der Koordinaten reduziert sich auf 21. Schließlich mit
 |
(4)
|
20 unabhängige Komponenten verbleiben (Misner et al. 1973, S. 220-221;Arfken 1985, S. 123-124).
Im Allgemeinen ist die Anzahl der unabhängigen Komponenten in 
Dimensionen gegeben durch
 |
(5)
|
die „vierdimensionalen Pyramidenzahlen“, deren erste Werte 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Die Anzahl der Skalare, die aus 
und 
konstruiert werden können, ist
 |
(6)
|
( Weinberg 1972). Die ersten Werte sind dann 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).
In Bezug auf den Jacobi-Tensor 
,
 |
(7)
|
Lassen
 |
(8)
|
wobei die Menge innerhalb der 
ein Christoffel-Symbol der zweiten Art ist. Dann
 |
(9)
|
Zerlegt in seine einfachste Zerlegung in 
Dimensionen,
 |
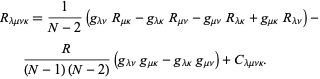(10)
|
Hier ist 
der Ricci-Krümmungstensor, 
ist die skalare Krümmung und 
ist der Weyl-Tensor.