yksinkertainen selitys verkkovaikutusten ”laille”
Metcalfen lain TLDR-selitys on, että verkkojen kasvaessa suuremmaksi niiden arvo kasvaa paljon käyttäjäkuntaa suuremmaksi ja nopeammaksi. Haluan mennä yhden tason syvemmälle ja antaa selityksen käyttäen yksinkertaista matematiikkaa.
ensinnäkin se auttaa ajattelemaan Metcalfen lakia kehyksenä sille, miten verkon arvoa voi ajatella. Aivan kuten Econ 101: ssä, opit tarjonnasta ja kysynnästä täydellisen kilpailun alla (mikään ei ole täydellistä), sinun pitäisi käsitellä tätä mallina ajatella verkon arvoa eikä yhtälöä, jota voit käyttää suoraan kättelyssä tosielämässä.
Tässä muutamia perusoletuksia mallin yksinkertaistamiseksi:
- ajattele tätä esimerkkiä tietoliikenneverkkona (esim. puhelimet tai telekopiolaitteet)
- verkon arvo mitataan yksinkertaisesti liittymien määrällä
- kunkin yhteyden arvo on sama
käytetään esimerkkinä fakseja. Yksinkertainen ajatus on, että jos useammilla ystävilläni on fakseja, voimme kaikki faksata toisillemme tavaroita ja saamme siitä arvoa.
seuraavaksi lasketaan mahdollisten yhteyksien määrä telekopiolaitteiden välillä:

tässä havainnollisia esimerkkejä:

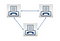
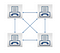
jos toistat tätä jatkuvasti, päädyt tällaiseen taulukkoon:

olisin voinut jatkaa, mutta pysähdyin 15-vuotiaana, koska on selvää, että mahdollisten yhteyksien määrä kasvaa paljon nopeammin kuin faksien määrä. Sarakkeen 1 ja sarakkeen 2 numeron välinen suhde osoittautuu:
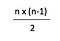
joten jos testaamme tätä käyttämällä 15 yllä olevasta taulukosta, meidän pitäisi saada 105:
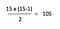
miten siis siirrytään yllä olevasta yhtälöstä ”n^2”: een? Lain mukaan verkon arvo on ”verrannollinen n ^2: een”. Helpoin tapa ajatella tätä on, että n saa isompi, ei ole paljon eroa ja .
joten se siitä.
kun viitekehys on ymmärretty, sitä voidaan alkaa repiä kappaleiksi: P
”entä jos omistan toisen kahdesta faksista maailmassa ja toisen omistaa arkkiviholliseni, enkä saa mitään arvoa tuosta yhteydestä?”
” entä jos mitä enemmän verkostoon liittyy ihmisiä, sitä saastuneemmaksi viestintäjärjestelmäni näyttää menevän?”
” jos käytän tätä kehystä yrittääkseni selvittää verkon rahakelpoista arvoa (tai yritysarvoa), sekoitanko kaksi hyvin erilaista asiaa?”
” miten tämä malli kestää, kun sovellan sitä sosiaalisiin verkostoihin enkä fakseihin?”