Si vous avez lu le post précédent sur ce qu’est une inductance, passons au niveau suivant, qu’est-ce que les circuits de formule d’inductance.
Maintenant que l’inducteur a été ajouté à notre liste d’éléments passifs, il est nécessaire d’étendre le puissant outil de combinaison série-parallèle. Nous devons savoir comment trouver l’inductance équivalente d’un ensemble d’inductances connectées en série ou en parallèle que l’on trouve dans des circuits pratiques.
Inductances en série
Considérons une connexion en série de N inductances, comme indiqué sur la figure.(1a), avec le circuit équivalent représenté sur la figure.(1 ter).

Les inducteurs ont le même courant à travers eux. Application de KVL à la boucle,

La substitution de vk = Lk di / dt entraîne des circuits de formule d’inductance
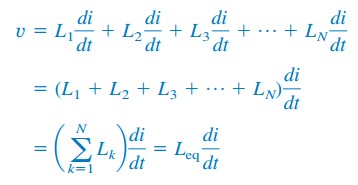
où

Ainsi,
L’inductance équivalente des inductances connectées en série est la somme des inductances individuelles.
Les inductances en série sont combinées exactement de la même manière que les résistances en série.
Inducteurs parallèles
Nous considérons maintenant une connexion parallèle de N inducteurs, comme le montre la figure.(2a), avec le circuit équivalent sur la figure.(2 ter). Les inducteurs ont la même tension aux bornes d’eux. En utilisant KCL,

Mais


par conséquent,

où
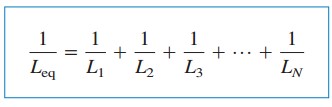
Le courant initial i(t0) traversant Leq à t = t0 est attendu par KCL comme la somme des courants d’inducteur à t0. Ainsi, selon l’équation.(5),
![]()
Selon l’équation.(6),
L’inductance équivalente des inductances parallèles est l’inverse de la somme des réciproques des inductances individuelles.
Notez que les inductances en parallèle sont combinées de la même manière que les résistances en parallèle.
Pour deux inducteurs en parallèle (N = 2), Équation.(6) devient
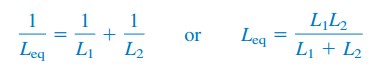
Exemples de Circuits de formule d’inductance
1. Trouvez l’inductance équivalente du circuit illustré sur la figure.(3).
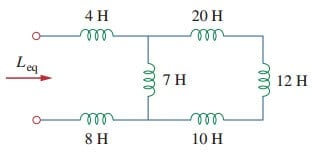
Solution :
Les inductances 10-H, 12-H et 20-H sont en série ; ainsi, les combiner donne une inductance de 42-H. Cet inducteur de 42 H est en parallèle avec l’inducteur de 7 H de sorte qu’ils sont combinés, pour donner des Circuits de Formule d’inductance


Cette inductance 6-H est en série avec les inductances 4-H et 8-H. Par conséquent,
![]()
2. Pour le circuit de la figure.(4),
i(t) = 4 (2−e−10t) mA. Si i2(0) = -1 mA, trouvez :
(a) i1(0);
(b) v(t), v1(t) et v2(t);
(c) i1(t) et i2(t).

Solution:
(a) De i (t) = 4 (2−e−10t) mA, i(0) = 4(2 − 1) = 4 Maman.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
( c) Le courant i1 est obtenu sous la forme de Circuits de Formule d’inductance


De même,


Notez que i1(t) + i2 (t) = i (t).