Le tenseur de Riemann (Schutz 1985) 
, également connu sous le nom de tenseur de courbure de Riemann-Christoffel (Weinberg 1972, p. 133; Arfken 1985, p. 123) ou tenseur de courbure de Riemann (Misner et al. 1973, p. 218), est un tenseur à quatre indices utile en relativité générale. D’autres tenseurs relativistes généraux importants tels que le tenseur de courbure de Ricci et la courbure scalaire peuvent être définis en termes de 
.
Le tenseur de Riemann est en quelque sorte le seul tenseur pouvant être construit à partir du tenseur métrique et de ses dérivées première et seconde,
 |
(1)
|
où 
sont des symboles de Christoffel du premier type et 
est un dérivé de virgule (Schmutzer 1968, p. 108; Weinberg 1972). Dans une dimension, 
. En quatre dimensions, il y a 256 composants. Utilisation des relations de symétrie,
 |
(2)
|
le nombre de composants indépendants est réduit à 36. Utilisation de la condition
 |
(3)
|
le nombre de coordonnées se réduit à 21. Enfin, en utilisant
 |
(4)
|
20 des composants indépendants sont laissés (Misner et al. 1973, p. 220-221; Arfken 1985, p. 123-124).
En général, le nombre de composants indépendants dans les dimensions 
est donné par
 |
(5)
|
les » nombres pyramidaux à quatre dimensions « , dont les premières valeurs sont 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (SIEO A002415). Le nombre de scalaires qui peuvent être construits à partir de 
et 
est
 |
(6)
|
( Weinberg 1972). Les premières valeurs sont alors 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (SIEO A050297).
En termes de tenseur de Jacobi 
,
 |
(7)
|
Laissez
 |
(8)
|
où la quantité à l’intérieur du 
est un symbole Christoffel du second type. Puis
 |
(9)
|
Décomposé dans sa décomposition la plus simple en dimensions 
,
 |
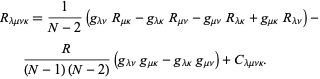(10)
|
Ici, 
est le tenseur de courbure de Ricci, 
est la courbure scalaire et 
est le tenseur de Weyl.