ha elolvasta az előző bejegyzést arról, hogy mi az induktor, folytassuk a következő szintre, mi az induktivitás képlet áramkörök.
most, hogy az induktor felkerült a passzív elemek listájára, ki kell terjeszteni a sorozat-párhuzamos kombináció hatékony eszközét. Tudnunk kell, hogyan lehet megtalálni a gyakorlati áramkörökben található soros vagy párhuzamosan csatlakoztatott induktorok ekvivalens induktivitását.
Soros induktorok
fontolja meg az n induktorok soros csatlakoztatását, az ábrán látható módon.(1a), az ábrán látható egyenértékű áramkörrel.(1b).

az induktorok azonos árammal rendelkeznek rajtuk keresztül. KVL alkalmazása a hurokra,

A vk= Lk di/dt helyettesítése
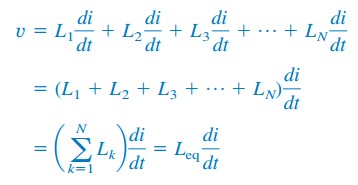
ahol

így,
a sorozathoz kapcsolt induktorok ekvivalens induktivitása az egyes induktivitások összege.
a Soros induktorokat pontosan ugyanúgy kombinálják, mint a Soros ellenállásokat.
párhuzamos induktorok
most az n induktorok párhuzamos csatlakoztatását vesszük figyelembe, amint az az ábrán látható.(2a), az ábrán látható egyenértékű áramkörrel.(2b). Az induktorok azonos feszültséggel rendelkeznek. KCL,

de


ezért

ahol
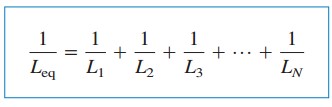
a kezdeti áram i (t0) keresztül Leq nál nél t= t0 várhatóan KCL az induktoráramok összege t0. Így az egyenlet szerint.(5),
![]()
egyenlet szerint.(6),
a párhuzamos induktorok ekvivalens induktivitása az egyes induktivitások reciproka összegének reciproka.
vegye figyelembe, hogy a párhuzamos induktorokat ugyanúgy kombinálják, mint a párhuzamos ellenállásokat.
két párhuzamos induktor esetében (N = 2), egyenlet.(6)
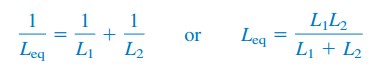
induktivitás képlet áramkörök példák
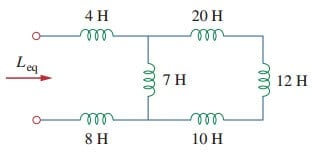
1. Keresse meg az ábrán látható áramkör ekvivalens induktivitását.(3).
megoldás:
a 10-H, 12-H és 20-H induktorok sorban vannak, így ezek kombinálása 42-H induktivitást eredményez. Ez a 42 órás induktor párhuzamosan van a 7 órás induktorral, így kombinálva


ez a 6 órás induktor sorban van a 4-H és 8-H induktorokkal. Ezért,
![]()
2. Az ábrán látható áramkör számára.(4),
i(t) = 4(2 − e−10t) mA. Ha i2 (0) = -1 mA, keresse meg:
(a) i1(0);
(b) v(t), v1(t) és v2(t);
(c) i1(t) és i2(t).

megoldás:
(a) i(t) = 4(2 − e−10t) mA, i(0) = 4(2 − 1) = 4 anya.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(c) az I1 áramot


hasonlóképpen,


vegye figyelembe, hogy i1(t) + i2(t) = i(t).