INTRODUZIONE
Competing risks (CR) è stato riconosciuto come un caso speciale di analisi time-to-event dal 18 ° secolo. Occasionalmente il lavoro in campo statistico o matematico è stato pubblicato incorporando nuovi sviluppi, tra cui la monografia di David e Moeschberger.1 Man mano che i dati diventavano più estesi, chiari e precisi per quanto riguarda i diversi tipi di risultati, il CR è riemerso come un tipo di analisi cruciale nell’analisi time-to-event, necessaria per una migliore comprensione di una malattia. La connessione tra i risultati matematici e il campo applicato doveva essere fatta. Diversi autori hanno contribuito alla comprensione delle situazioni CR.2, 3 Altri autori hanno migliorato e sviluppato tecniche e in alcuni casi reso disponibile il codice informatico pronto all’uso per le statistiche applicate.4, 5, 6
INTRODUZIONE ALL’ANALISI TIME-TO-EVENT
In molti studi il risultato è osservato longitudinalmente. In questo modo ogni soggetto della coorte viene osservato per un periodo di tempo fino a quando non si verifica l’evento. Ad esempio l’evento di interesse può essere la morte, infarto o recidiva del cancro. Gli obiettivi dello studio possono essere quelli di stimare la probabilità che l’evento si verifichi o la sua associazione con covariate di interesse come il trattamento o le caratteristiche del soggetto. L’analisi statistica impiegata è chiamata analisi time-to-event o talvolta analisi di sopravvivenza. Il metodo più comune per stimare la probabilità di un evento è un approccio non parametrico solitamente chiamato metodo Kaplan-Meier7 (KM) o limite di prodotto. L’ipotesi principale della stima KM per la sopravvivenza è che le osservazioni censurate sperimenteranno l’evento se seguite abbastanza a lungo.
Per il resto di questo documento, verranno fornite le probabilità per l’evento piuttosto che la probabilità per l’evento gratuito. Ad esempio, invece della probabilità di sopravvivenza, verrà presentata la probabilità di morte, che può essere stimata utilizzando il complemento dello stimatore KM: 1-KM.
INTRODUZIONE AI RISCHI CONCORRENTI
Non è raro che un partecipante a uno studio sperimenta più di un tipo di evento. Una situazione CR si verifica quando il verificarsi di un tipo di evento cambia la capacità di osservare l’evento di interesse. Miyasaka et al.8 ha condotto uno studio su una coorte di pazienti con diagnosi di fibrillazione atriale tra il 1986 e il 2000 nella contea di Olmsted, Minnesota, Stati Uniti. Il risultato primario era l’insorgenza della demenza. Il follow-up mediano è stato di 4,6 anni. Altri tipi di eventi erano ictus e morte. Dei 2837 individui con fibrillazione atriale, 299 avevano demenza e 1638 morirono al momento dell’analisi. I numeri con ictus non sono riportati e sono censurati nell’analisi. La conclusione dello studio è stata che l’incidenza di demenza tra gli individui con fibrillazione atriale è comune (10,5% a 5 anni utilizzando il metodo KM). L’insorgenza di ictus prima della demenza non influisce sull’osservazione della demenza e quindi non è un evento CR. Per ragioni di discussione ignoriamo il fatto che più ictus possono causare demenza. D’altra parte, una morte senza demenza precedente rende impossibile l’osservazione della demenza. Pertanto, una morte senza demenza è un evento CR per l’endpoint della demenza. Anche una grave lesione alla testa potrebbe essere considerata un evento CR poiché i cambiamenti comportamentali del paziente potrebbero rendere impossibile la diagnosi di demenza.
Una situazione CR più sottile si verifica nello studio condotto da Whalley et al.9 dell’importanza dell’ecocardiografia. Questa coorte di pazienti sintomatici anziani 228 è stata sottoposta a ecocardiografia ed è stata seguita per ospedalizzazione cardiovascolare o morte cardiovascolare. L’ipotesi era che le caratteristiche di ecocardiografia predicono per evento cardiovascolare. Il risultato principale è stato definito come la misura composita comprendente la morte cardiovascolare e / o il ricovero in ospedale. Per questo tipo di esito una morte dovuta a cause diverse dalla malattia cardiovascolare è un evento CR e, come tale, un paziente non è più a rischio di avere uno qualsiasi degli eventi di interesse.
Uno studio randomizzato a 3 bracci, in doppio cieco, è stato condotto in 931 centri e 24 paesi per testare l’effetto di valsartan vs valsartan+captopril vs captopril alone (VALIANT)10 sulla mortalità per tutte le cause. In totale, 14 703 pazienti post-infarto miocardico con disfunzione del ventricolo sinistro e / o insufficienza cardiaca accumulati 1:1:1 nei 3 bracci. Poiché ogni morte è stata considerata un evento, questo tipo di risultato non ha CR. Lo studio ha sostenuto l’ipotesi che la sopravvivenza nei bracci 3 fosse diversa. Tuttavia, il sanguinamento gastrointestinale (GI) è stato identificato come un grave effetto indesiderato in tutti e 3 i bracci. Moukarbel et al.11 ha studiato i possibili fattori che potrebbero predire il sanguinamento gastrointestinale. Per questo endpoint, la morte senza sanguinamento gastrointestinale è un CR chiaro.
Un numero crescente di ricercatori riconosce la presenza di CR e la necessità di tecniche adeguate da applicare. Una coorte di 972 pazienti con sindrome coronarica acuta senza elevazione del segmento ST tra il 2001 e il 2005 è stata studiata da Núñez et al.12 Uno degli obiettivi dello studio era quello di trovare fattori associati alla reospitalizzazione per insufficienza cardiaca acuta. Tra i fattori studiati c’erano il diabete, la precedente storia di cardiopatia ischemica, l’insufficienza renale cronica, la storia del fumo e la storia del trattamento. Gli autori hanno riconosciuto la possibilità di CR come la morte prima della reospitalizzazione e hanno applicato correttamente tecniche specifiche per spiegare la situazione CR.
Melberg et al.13 ha studiato una coorte di 1234 pazienti con malattia coronarica sintomatica che hanno ricevuto 2 tipi di trattamenti: innesto di bypass coronarico (n=594) o intervento coronarico percutaneo (n=640). Dei 301 decessi osservati durante il follow-up, il 42,5% erano decessi cardiaci e il resto erano decessi non cardiaci. Gli autori presentano risultati per la mortalità per tutte le cause, nonché per la mortalità cardiaca e la mortalità non cardiaca. Sottolineano che la percentuale di mortalità per tutte le cause è la somma della percentuale di mortalità cardiaca e non cardiaca correttamente stimata tenendo conto del CR. Gli autori sottolineano l’importanza di analizzare ciascuno degli eventi di interesse piuttosto che combinarli in una mortalità complessiva. Questo argomento è anche esposto a un livello più generale da Mell e Jeong.14
Come si può supporre dagli esempi precedenti, la domanda principale quando sono presenti CR è se ignorare il CR e censurare le osservazioni che coinvolgono CR o tenere conto di CR. Quando le CR vengono ignorate e le osservazioni CR vengono censurate, l’analisi si riduce a un “solito” scenario time-to-event. A causa della familiarità di questo tipo di analisi e della disponibilità di software, molti ricercatori ricorrono a questo approccio, come visto negli esempi precedenti. Tuttavia, è unanimemente concordato non solo tra gli statistici2, 15, 16, 17, 18 che la stima della probabilità di evento in questo caso sopravvaluta la vera probabilità. La prossima domanda naturale è se la modellazione può essere eseguita entro questi limiti (ignorando/censurando CR). Questo è più ambiguo e più difficile da afferrare. Mentre tale analisi potrebbe non essere priva di valore, la sua interpretazione è quasi sempre irta di difficoltà. Il requisito principale è che l’evento CR (le cui osservazioni sono state censurate e mescolate con le vere osservazioni censurate) debba essere indipendente dall’evento di interesse. Se questo è il caso, i risultati potrebbero essere interpretati come l’effetto delle covariate quando gli eventi CR non esistevano. Tuttavia, questa ipotesi di solito non può essere fatta e non può essere verificata o testata. In conclusione, ogni volta che le osservazioni CR vengono censurate la stima della probabilità di evento è errata e l’interpretazione dell’effetto delle covariate non è chiara a causa della mancanza di conoscenza dell’indipendenza tra l’evento di interesse e l’evento CR.
Quando l’analisi viene eseguita tenendo conto del CR (e codificata distintamente dall’evento di interesse o dalla censura), la probabilità viene correttamente stimata e la modellazione ha un’interpretazione diretta. Non vi è alcuna assunzione di indipendenza per ostacolare l’interpretazione. Il coefficiente di una covariata così stimato rappresenta l’effetto di tale covariata sulle probabilità osservate.
Diversi autori19, 20 hanno tentato di confrontare i due approcci in termini di potenza dei test utilizzando simulazioni. Tuttavia, il ricercatore deve essere consapevole che il problema principale è nell’interpretazione dei risultati. Indipendentemente dalla potenza dei test, l’analisi deve rispondere alla domanda dello studio.
STIMA DELLA PROBABILITÀ DI EVENTO
È pratica comune applicare il metodo KM per stimare la probabilità di un evento. La formula tipica per la stima KM è
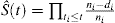
, dove t1t2t3ni rappresenta il numero di pazienti a rischio al momento ti e di è il numero di eventi al momento ti.
Questa formula può essere trasformato attraverso la manipolazione algebrica di esprimere la probabilità di un evento come:
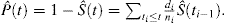
In presenza di CR ci sono almeno 2 tipi di eventi: evento di interesse, identificato con il pedice e, e i concorrenti evento a rischio, identificato con il pedice c. Kalbfleisch e Prentice hanno introdotto la formula per la probabilità di un evento di interesse in presenza di CR:
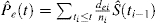
È interessante notare la relazione tra (1) e (2). Poiché di è il numero di tutti gli eventi a ti, può essere concepito come la somma del numero di eventi di interesse dei e il numero di eventi CR dci al tempo ti. Come tale, la probabilità di qualsiasi tipo di evento può essere scomposta come:
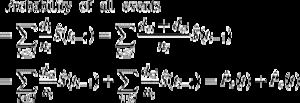
Quindi la probabilità di tutti gli eventi può essere scomposta nelle probabilità per ogni tipo di evento.
Se si utilizza 1-KM per calcolare la probabilità di un evento di interesse in presenza di CR, la sopravvivenza di tutti gli eventi nella formula (2) è sostituita dalla stima del KM basata solo sugli eventi di interesse. Questo influenzerà i risultati, come verrà mostrato in seguito. L’ipotesi principale per l’uso del metodo KM è che i pazienti censurati, se seguiti abbastanza a lungo, alla fine sperimenteranno l’evento. Tuttavia, quando il metodo KM viene utilizzato in presenza di CR, i pazienti che presentano tipi di eventi diversi dall’evento di interesse vengono solitamente censurati, anche se non sono più a rischio per l’evento di interesse. Inoltre, la bella decomposizione vista in (3) non può essere eseguita per la formula 1-KM.
In situazioni applicate è possibile che ci siano diversi altri tipi di eventi che non sono di interesse. In questo caso tutti possono essere raggruppati sotto l’ombrello di eventi CR.
Verrà mostrato attraverso un esempio che l’uso del metodo KM non è appropriato in presenza di CR.
Descrizione dell’esempio
Un set di dati raccolti per studiare gli effetti tardivi del trattamento per il linfoma di Hodgkin sarà utilizzato per l’illustrazione. Il risultato principale è il ricovero in ospedale per malattie cardiache. Il linfoma di Hodgkin è un tipo di cancro che appare soprattutto nei giovani adulti. Nelle sue fasi iniziali è quasi curabile, con una sopravvivenza globale di 10 anni del 70%. Pertanto, una coorte di questi pazienti è ideale per studiare gli effetti collaterali a lungo termine del trattamento. Il set di dati utilizzato qui è un sottoinsieme di una coorte più ampia che verrà riportata altrove. I dati vengono anche modificati per servire i nostri scopi. Ad esempio, per semplicità, abbiamo tenuto nei dati solo i pazienti che avevano chemioterapia o radioterapia, esclusi quelli con trattamento combinato. Per aumentare il tasso di CR (morte senza ospedalizzazione cardiaca), abbiamo incluso pazienti di tutte le fasi. Alcune date di follow-up e morte sono stati imputati. A causa delle modifiche apportate ai dati, non è possibile trarre conclusioni cliniche da questa analisi. I dati presentati qui fanno riferimento a 689 record con 93 ricoveri cardiaci e 467 decessi.
I tassi di ospedalizzazione cardiaca e di morte senza evento cardiaco saranno calcolati utilizzando sia il metodo KM (1) che la funzione di incidenza cumulativa (CIF) introdotta da Kalbfleisch e Prentice21 a tale scopo (2).
Il metodo Kaplan-Meier Applicato a una situazione di rischio concorrente Sovrastima il tasso reale dell’evento
La figura 1 presenta le stime CIF e 1-KM per l’ospedalizzazione cardiaca del gruppo trattato solo con chemioterapia. La linea spezzata corrispondente alle stime di 1 KM è superiore alla linea continua che rappresenta le stime CIF. Si può dimostrare matematicamente che 1 KM sopravvaluta sempre la probabilità di evento. Un malinteso comune è che le stime di 1 KM siano corrette se i due eventi sono indipendenti. L’indipendenza tra gli eventi è sempre discutibile nella migliore delle ipotesi, ma anche quando i dati vengono simulati come eventi indipendenti, esiste la differenza tra le stime CIF e 1-KM. La dimensione della differenza dipende dal numero di eventi, sia per gli eventi di interesse che per gli eventi CR. In Miyasaka et al., 8 l’incidenza di demenza a 5 anni usando il metodo KM era del 10,5%. Il numero di CR (morti) era circa tre quarti del numero totale di eventi, il che suggerisce che la loro stima potrebbe essere molto più grande di quella osservata.
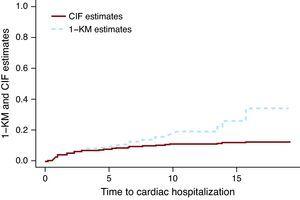
Figura 1. Funzione di incidenza cumulativa vs stime 1-Kaplan-Meier.. CIF, funzione di incidenza cumulativa; KM, Kaplan-Meier.
La funzione di incidenza cumulativa divide la probabilità di qualsiasi evento (ospedalizzazione cardiaca o morte) nelle probabilità costituenti
Algebricamente questo è dimostrato in (3). Tuttavia, per una comprensione più profonda di come funziona, verrà mostrato graficamente che dalla probabilità di tutti gli eventi una parte partecipa al CIF per un evento e l’altro al CIF per l’altro evento. La figura 2A mostra la probabilità di qualsiasi evento: ospedalizzazione cardiaca o morte senza ospedalizzazione cardiaca. La figura 2B contiene solo la curva compresa tra 10,7 e 10.85 anni, in modo tale che i passaggi siano visibili. Su ogni passo c’è un cerchio. I cerchi aperti appaiono sui gradini in cui è stata osservata una morte mentre i cerchi solidi si trovano sui gradini in cui si è verificato un ricovero cardiaco. I passi con cerchi solidi partecipano al CIF per l’ospedalizzazione cardiaca nel pannello C e quelli con cerchi aperti partecipano alla curva per la morte in Figura 2D. Quindi, ogni passo contribuirà alla probabilità dell’evento che lo causa. In questo modo, in qualsiasi momento la probabilità di tutti gli eventi è la somma della probabilità dell’evento di interesse e della probabilità di CR. Si noti che gli ultimi 3 pannelli (Figura 2B-D) mostrano la stessa finestra di tempo e hanno la stessa lunghezza per l’asse y in modo tale che la dimensione dei passaggi possa essere confrontata tra loro. La tabella 1 mostra queste probabilità a 1, 2, 3, 4 e 5 anni.
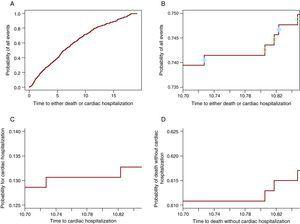
Figura 2. La partizione della probabilità di tutti gli eventi nelle probabilità costituenti. A. La probabilità di ospedalizzazione cardiaca o morte. B. La probabilità di ospedalizzazione cardiaca o morte solo per la finestra di tempo 10,70 – 10,85 anni. I cerchi solidi indicano l’ospedalizzazione cardiaca e i cerchi aperti rappresentano morti senza ospedalizzazione cardiaca. C. La probabilità di ospedalizzazione cardiaca nella finestra di tempo 10,70 -10,85 anni. D. La probabilità di morte senza ricovero cardiaco nella finestra di tempo 10.70-10.85.
Tabella 1. La Probabilità per ogni evento è la Somma delle probabilità costituenti.
| Anno di reporting | Probabilità di cardiaco ricovero | Probabilità di morte | Probabilità di risultare cardiaco ospedalizzazione o di morte |
| 1 | 0.038 | 0.054 | 0.092 |
| 2 | 0.054 | 0.139 | 0.193 |
| 3 | 0.072 | 0.193 | 0.265 |
| 4 | 0.076 | 0.25 | 0.327 |
| 5 | 0.087 | 0.305 | 0.392 |
Poiché il KM 1 sopravvaluta la probabilità di un evento, se provassimo ad aggiungere le stime del KM 1 per l’ospedalizzazione cardiaca al KM 1 per la morte otterremmo un tasso molto più alto della probabilità di qualsiasi evento. In alcuni casi il numero ottenuto è anche maggiore di 1, il che dimostra che in presenza di CR, le stime di 1 KM non sono nemmeno probabilità.
Il metodo della funzione di incidenza cumulativa stima effettivamente la probabilità corretta dell’evento?
A questo scopo è stato simulato un set di dati di 500 record in modo tale che non vi sia alcuna censura prima di 5 anni e ci sono 2 tipi di eventi: tipo 1 e 2. La tabella 2 mostra per ogni tipo di evento il numero osservato fino a quel momento, il tasso grezzo e la stima CIF, che sono esattamente uguali. L’uguaglianza avviene solo quando non ci sono osservazioni censurate fino a quel momento. In presenza di osservazioni censurate entro gli anni riportati l’uguaglianza non vale e il modo corretto per stimare la probabilità è il CIF e non il tasso grezzo.
Tabella 2. La probabilità dei due tipi di evento quando non ci sono osservazioni censurate fino a 5 anni.
CIF, funzione di incidenza cumulativa.
In conclusione, per calcolare la probabilità di evento in presenza di CR si deve utilizzare il metodo introdotto da Kalbfleisch e Prentice, comunemente chiamato curva di incidenza cumulativa.
MODELLAZIONE
Un aspetto importante in un’analisi è quello di testare l’associazione tra una covariata e l’evento di interesse, da solo o regolando per altri fattori. In assenza di CR, ciò viene eseguito di routine utilizzando il modello Cox proportional hazards (Cox PH).22
In presenza di CR, il modello Cox PH non ha una semplice interpretazione. Se il tempo per i 2 tipi di eventi può essere considerato indipendente, i risultati possono essere interpretati come mostrando l’effetto nella situazione in cui CR non esiste. Tuttavia, l’ipotesi di indipendenza può raramente essere fatta o testata e quindi i risultati del modello di Cox PH non sono solitamente interpretabili.
Modello Fine e Grigio
Fine e Gray6 (F&G) hanno modificato il modello Cox PH per consentire la presenza di CR. La modifica tecnica consiste nel mantenere le osservazioni CR nel rischio impostato con un peso decrescente. In questo modo il metodo F&G modella i pericoli di sottodistribuzione. L’effetto stimato utilizzando il modello F & G mostra le differenze attuali e reali tra i gruppi di trattamento in termini di rapporti di rischio di sottodistribuzione. L’assunzione di proporzionalità dei rischi è ancora un requisito, ma ovviamente si riferisce ai rischi di sottodistribuzione. Il modello F & G può contenere coefficienti dipendenti dal tempo per modellare la non proporzionalità dei pericoli. Questo modello può essere applicato sia all’evento di interesse (ospedalizzazione cardiaca) che al CR (morte).
I modelli Cox PH e F& G sono stati applicati al set di dati sul linfoma di Hodgkin per testare l’opzione di trattamento della chemioterapia rispetto alle radiazioni. Per questo esempio (Tabella 3) i risultati dei modelli Cox PH e F&G differiscono sostanzialmente (prime 2 righe). Come accennato in precedenza, i risultati di Cox PH non sono interpretabili e non possono essere utilizzati. La seconda fila mostra che ci sono più ricoveri cardiaci tra il gruppo di radiazioni e la terza fila mostra più morti tra il gruppo chemioterapico. La figura 3 mostra questi risultati graficamente. È possibile che la chemioterapia da sola sia stata somministrata a pazienti con malattia più avanzata, e questi pazienti avevano anche maggiori probabilità di morire di cancro. D’altra parte la sola radiazione è stata probabilmente somministrata a pazienti in una fase precoce che hanno vissuto più a lungo dopo la diagnosi di linfoma di Hodgkin. Questi pazienti avevano più possibilità di sviluppare effetti collaterali tardivi come la malattia cardiaca.
Tabella 3. L’effetto del trattamento quando vengono impiegati rischi proporzionali alla Cox e modelli fini e grigi.
CI, intervallo di confidenza; Cox PH, Cox proporzionali pericoli modello; F & G, Fine e grigio modello; HR, hazard ratio.
Gli hazard ratio mostrano l’aumento dei pericoli per il gruppo di radiazioni rispetto al gruppo chemioterapico.
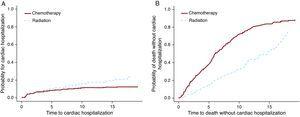
Figura 3. L’effetto del trattamento per l’ospedalizzazione cardiaca e per la morte.
Come si può vedere da questo esempio, l’interpretazione dei risultati è un lavoro di collaborazione tra lo statistico e il clinico che ha una conoscenza approfondita della malattia.
La presenza di CR complica sia l’analisi che l’interpretazione dei dati. Per consentire al lettore di interpretare correttamente i risultati, gli autori devono includere dettagli sugli eventi osservati anche se potrebbero non sembrare importanti a prima vista. Pertanto, quando l’endpoint viene osservato nel tempo, gli autori devono includere l’evento di interesse, se esiste la possibilità di CR, quanti pazienti sperimentano uno di questi tipi di eventi e la durata del follow-up. In presenza di CR è informativo includere l’analisi per l’evento di interesse e l’analisi per CR, in quanto si completano a vicenda e potrebbero aiutare a interpretare i risultati.
L’approccio logistico
Supponiamo innanzitutto di essere nel quadro di nessun CR. Quando si prevede che il risultato si verifichi entro un breve intervallo (ad esempio, 1 anno), lo strumento di scelta per molti ricercatori è la regressione logistica. Questo è appropriato se ogni individuo nella coorte ha il follow-up minimo, in questo caso 1 anno. Infatti la stima per la mortalità di 1 anno coinciderà con la stima di 1 KM. Il punto di cut-off temporale deve essere lo stesso per ogni individuo nella coorte. Pertanto, se il risultato di interesse è la mortalità di 1 anno e 1 individuo nella coorte muore a 1 anno e 2 giorni, quella persona dovrebbe essere considerata come “nessun evento a 1 anno.”Questo può ridurre il numero di eventi, che si traduce in un’analisi meno ideale quando molti eventi osservati si verificano dopo il punto di cut-off.
Le stesse regole di base si applicano quando sono presenti CR. Tutti gli individui della coorte devono avere il follow-up minimo scelto come punto di interruzione del tempo e tale punto di interruzione deve essere applicato a tutti nella coorte. I coefficienti e i valori p daranno in generale lo stesso messaggio ma non saranno esattamente gli stessi per la regressione logistica rispetto al modello F&G. Innanzitutto, nella regressione logistica il coefficiente rappresenta il log dell’odds ratio, mentre nel modello F & G è il log del ratio delle sottodistribuzioni dei pericoli. Inoltre, nell’analisi logistica non vengono utilizzati tutti gli eventi e, naturalmente, viene utilizzato un modello diverso.
CALCOLO DELLA POTENZA
Quando la misura è time-to-event, il calcolo della potenza ha due fasi. Il primo passo è calcolare il numero di eventi necessari per rilevare una dimensione specifica dell’effetto. Successivamente, viene calcolato il numero di pazienti necessari per osservare tale numero di eventi. È stato sottolineato nelle sezioni precedenti che quando CR sono presenti non è possibile osservare tutti gli eventi di interesse dovuti al verificarsi di CR. Poiché il numero di eventi è centrale nel calcolo della potenza, è necessario prestare particolare attenzione per garantire che le CR siano prese in considerazione. Se le CR non vengono prese in considerazione, lo studio sarà sottodimensionato e quindi probabilmente infruttuoso (e possibilmente non etico).
SOFTWARE
Il software R open source sul sito CRAN (the Comprehensive R Archive Network) (http://cran.r-project.org/) offre un pacchetto (cmprsk) implementato dal Dr. Robert Gray contenente gli strumenti necessari per una contabilità analisi completa per CR. Pertanto, si potrebbero ottenere grafici di probabilità osservati per l’evento di interesse e un valore p basato sul test di Gray, che è un test logrank modificato per la situazione CR. All’interno del pacchetto c’è anche una funzione per la modellazione utilizzando l’approccio F&G. Luca Scruca ha migliorato la consegna in uscita della funzione di modellazione per una più facile lettura incorporando nel pacchetto una funzione di tipo di riepilogo. Il modello ha la possibilità di verificare la proporzionalità dei pericoli e possono essere inclusi i termini per i coefficienti dipendenti dal tempo. Il codice non può contenere dati di troncamento sinistro o cluster. Il troncamento a sinistra sarebbe utile per l’analisi di eventi multipli/ricorrenti per paziente o per l’analisi della coorte dei casi. È stato sviluppato un codice per gli studi caso-coorte (Pintilie et al.23) e può essere ottenuto dagli autori. Zhou et al.24 esteso il modello F & G per ospitare dati stratificati e avrà anche una versione per i dati del cluster. A questo punto il codice può essere ottenuto dagli autori per entrambi i casi, ma è probabile che sarà presentato al CRAN.
STATA 11 ha recentemente implementato il modello F&G. Bisogna essere consapevoli che i grafici ottenuti usando STATA sono predittivi piuttosto che grafici di probabilità osservati. Ci sono due avvertimenti quando vengono utilizzate le curve previste: a) le linee appariranno sempre come se la proporzionalità dei pericoli fosse soddisfatta e b) il numero di passi in ogni curva sarà maggiore del numero di eventi in ciascun sottogruppo, dando l’impressione che ci siano più eventi di quanti ce ne siano realmente.
CONCLUSIONI
La disponibilità di set di dati di grandi dimensioni con follow-up completo per diversi endpoint è in continuo aumento. Vi è anche una crescente necessità di analisi che riguardano un endpoint preciso come la morte per insufficienza cardiaca o il controllo della malattia o il controllo della malattia locale. Tutti questi endpoint potrebbero potenzialmente avere CR. Pertanto è essenziale che il CR sia considerato dalla fase di progettazione all’interpretazione dei risultati. Mentre il modello di Cox PH può avere un valore limitato quando si considera l’indipendenza, le stime KM non sono corrette e non possono essere interpretate. Pertanto, devono essere applicate tecniche specifiche come i modelli CIF e F&G resi disponibili in R e parzialmente in STATA.
CONFLITTI DI INTERESSE
Nessuno dichiarato.