Se avete letto il post precedente su ciò che è un induttore, passiamo al livello successivo, qual è la formula induttanza circuits.
Ora che l’induttore è stato aggiunto alla nostra lista di elementi passivi, è necessario estendere il potente strumento di combinazione serie-parallelo. Abbiamo bisogno di sapere come trovare l’induttanza equivalente di un insieme di induttori collegati in serie o collegati in parallelo che si trovano nei circuiti pratici.
Serie Induttori
Si consideri un collegamento in serie di N induttori, come mostrato in figura.(1a), con il circuito equivalente mostrato in Figura.(1 ter).

Gli induttori hanno la stessa corrente attraverso di loro. Applicando la KVL alla rete,

Sostituendo vk= Lc di/dt risultati in
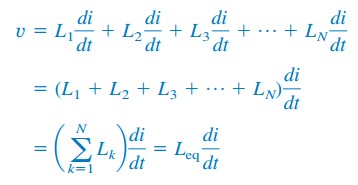
dove

Così,
L’equivalente induttanza collegati in serie induttori è la somma delle singole induttanze.
Gli induttori in serie sono combinati esattamente allo stesso modo dei resistori in serie.
Induttori paralleli
Consideriamo ora una connessione parallela di N induttori, come mostrato in Figura.(2a), con il circuito equivalente in Figura.(2 ter). Gli induttori hanno la stessa tensione su di loro. Utilizzando KCL,

Ma


quindi

dove
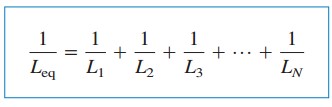
La corrente iniziale i(t0) attraverso Leq a t= t0 è previsto da KCL essere la somma dell’induttore correnti a t0. Quindi, secondo l’equazione.(5),
![]()
Secondo l’equazione.(6),
L’induttanza equivalente degli induttori paralleli è il reciproco della somma dei reciproci delle singole induttanze.
Si noti che gli induttori in parallelo sono combinati allo stesso modo dei resistori in parallelo.
Per due induttori in parallelo (N = 2), Equazione.(6) diventa
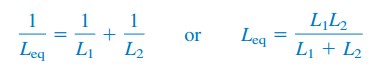
Induttanza Formula Circuiti Esempi
1. Trova l’induttanza equivalente del circuito mostrato in Figura.(3).
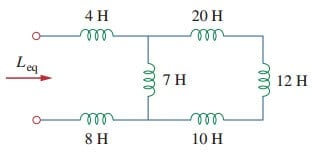
Soluzione:
Gli induttori 10-H, 12-H e 20-H sono in serie; quindi, combinandoli, si ottiene un’induttanza 42-H. Questo 42-H induttore è in parallelo con il 7-H induttore in modo che essi sono combinati,per dare


Questo induttore 6-H è in serie con gli induttori 4-H e 8-H. Quindi,
![]()
2. Per il circuito in Figura.(4),
i (t) = 4 (2−e-10t) mA. Se i2(0) = -1 mA, trovare:
(a) i1(0);
(b) v(t), v1(t) e v2(t);
(c) i1(t) e i2 (t).

Soluzione:
(a) Da i (t) = 4 (2−e-10t) mA, i(0) = 4(2 − 1) = 4 Mamma.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(c) La corrente i1 è ottenuto come


allo stesso modo,


Nota che i1(t) + i2(t) = i(t).