Il tensore di Riemann (Schutz 1985) 
, noto anche Riemann-Christoffel tensore di curvatura (Weinberg, 1972, p. 133; Arfken 1985, p. 123) o tensore di curvatura di Riemann (Misner et al. 1973, p. 218), è un tensore a quattro indici che è utile nella relatività generale. Altri importanti tensori relativistici generali tali che il tensore di curvatura di Ricci e la curvatura scalare possono essere definiti in termini di 
.
Il tensore di Riemann è in un certo senso l’unico tensore che può essere costruito a partire dal tensore metrico e la prima e la seconda derivati,
 |
(1)
|
dove 
sono i simboli di Christoffel del primo tipo e 
è una virgola derivati (Schmutzer 1968, p. 108; Weinberg 1972). In una dimensione, 
. In quattro dimensioni, ci sono 256 componenti. Facendo uso delle relazioni di simmetria,
 |
(2)
|
il numero di componenti indipendenti è ridotto a 36. Utilizzando la condizione
 |
(3)
|
il numero di coordinate si riduce a 21. Infine, usando
 |
(4)
|
20 i componenti indipendenti sono lasciati (Misner et al. 1973, pp. 220-221;Arfken 1985, pp. 123-124).
In generale, il numero di componenti indipendenti in 
dimensioni è dato da
 |
(5)
|
il “four-dimensional piramidale numeri,”i primi valori di cui sono 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Il numero di scalari che può essere costruito a partire da 
e 
è
 |
(6)
|
(Weinberg 1972). I primi valori sono quindi 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).
In termini di tensore di Jacobi 
,
 |
(7)
|
Lasciate
 |
(8)
|
dove la quantità all’interno del 
è un simbolo di Christoffel di seconda specie. Allora
 |
(9)
|
suddivise in semplici decomposizione 
dimensioni,
 |
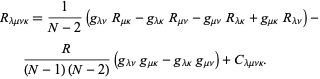(10)
|
Qui,
è il tensore di curvatura Ricci, 
è la curvatura scalare e
è il tensore di Weyl.