네트워크 효과의”법칙”에 대한 간단한 설명 멧 칼프의 법칙에 대한 설명은 네트워크가 커짐에 따라 사용자 기반보다 훨씬 더 크고 빠르게 가치가 증가한다는 것입니다. 나는 한 단계 더 깊이 가서 간단한 수학을 사용하여 설명을 제공하고 싶다.
우선,멧 칼프의 법칙을 네트워크의 가치에 대해 생각하는 방법의 틀로 생각하는 데 도움이됩니다. 경제학 101 에서 완벽한 경쟁에서 수요와 공급에 대해 배우는 것과 마찬가지로(완벽한 것은 없습니다),이것을 네트워크 가치에 대해 생각하는 모델로 취급해야하며 실제 생활에서 상자 밖으로 곧바로 사용할 수있는 방정식이 아닙니다.
모델을 단순화하기 위한 몇 가지 기본 가정은 다음과 같습니다:
- 이 예제를 통신 네트워크라고 생각하십시오(예: 각 연결의 값은 동일
의 팩스 기계의 예를 사용하자. 간단한 아이디어는 나의 친구의 더 많은 것이 복사 전송기가 있는 경우에,우리는 모두 재료를 팩스로 보낼 수 있고 우리 모두 그것에서 가치를 얻는다 이다.
다음으로 팩스 사이의 가능한 연결 수를 집계해 보겠습니다:

다음은 예시적인 예입니다:

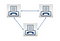
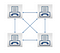
이 작업을 계속 반복하면 다음과 같은 테이블이 생깁니다:

가능한 연결의 수가 복사 전송기의 수보다는 매우 빠르게 성장하고 있다 고 명확하기 때문에 나는 가는 것을 계속하고 그러나 15 에 멈출 수 있었다. 열 1 과 열 2 의 숫자 사이의 관계는 다음과 같습니다:
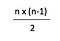
따라서 위의 표에서 15 를 사용하여 테스트하면 105 를 얻어야합니다:
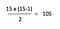
그렇다면 위의 방정식에서”엔^2″로 어떻게 이동합니까? 음,이 법은 네트워크의 가치가”엔^2 에 비례”라고 말합니다. 이것에 대해 생각하는 가장 쉬운 방법은 엔 점점 커짐에 따라 과 사이에 큰 차이가 없다는 것입니다.
그래서 정말입니다.
당신이 프레임 워크를 이해하면,우리는 그것을 찢어 시작할 수 있습니다:피
“만약 내가 세계에서 두 팩스 기계 중 하나를 소유 하 고 다른 내 대적에 의해 소유 하 고 그 연결에서 값을 얻을?”
“네트워크에 가입 더 많은 사람들이,더 오염 된 내 통신 시스템은 무엇을 얻을 것으로 보인다 경우?”
“이 프레임 워크를 사용하여 네트워크의 수익 창출 가치(또는 기업 가치)를 파악하면 매우 다른 두 가지를 결합하고 있습니까?”
“이 모델은 팩스가 아닌 소셜 네트워크에 적용 할 때 어떻게 유지됩니까?”