INTRODUCTION
Competing risks (CR) jest uznawany za Szczególny przypadek analizy time-to-event od XVIII wieku. Sporadycznie publikowane były prace z dziedziny statystyki lub matematyki zawierające nowe osiągnięcia, w tym monografię Davida i Moeschbergera.1 ponieważ dane stały się bardziej obszerne, jasne i precyzyjne w odniesieniu do różnych typów wyników, CR pojawił się jako kluczowy rodzaj analizy w analizie czasu do zdarzenia, niezbędny do lepszego zrozumienia choroby. Konieczne było nawiązanie połączenia między wynikami matematycznymi a zastosowanym polem. Kilku autorów przyczyniło się do zrozumienia sytuacji CR.2, 3 inni autorzy udoskonalali i rozwijali techniki, a w niektórych przypadkach udostępniali gotowy do użycia kod komputerowy do stosowanych statystyk.4, 5, 6
wprowadzenie do analizy czasu do zdarzenia
w wielu badaniach wynik jest obserwowany wzdłużnie. W ten sposób każdy podmiot w kohorcie jest obserwowany przez okres czasu, aż do wystąpienia zdarzenia. Na przykład interesującym wydarzeniem może być śmierć, zawał serca lub nawrót raka. Celem badania może być oszacowanie prawdopodobieństwa wystąpienia zdarzenia lub jego związku z współzmiennymi interesującymi, takimi jak leczenie lub cechy przedmiotu. Stosowana analiza statystyczna nazywana jest analizą czasu do zdarzenia lub czasem analizą przeżycia. Najczęstszą metodą szacowania prawdopodobieństwa wystąpienia zdarzenia jest nieparametryczne podejście zwyczajowo nazywane metodą Kaplana-Meier7 (KM) lub metodą granicy produktu. Głównym założeniem oceny przeżycia KM jest to, że ocenzurowane obserwacje doświadczą zdarzenia, jeśli będą odpowiednio długo śledzone.
w dalszej części tego artykułu, prawdopodobieństwo zdarzenia będzie podane, a nie prawdopodobieństwo zdarzenia wolnego od zdarzenia. Na przykład zamiast prawdopodobieństwa przeżycia zostanie przedstawione prawdopodobieństwo śmierci, które można oszacować za pomocą dopełniacza estymatora KM: 1-KM.
wprowadzenie do ryzyka konkurencyjnego
nierzadko zdarza się, że Uczestnik badania doświadcza więcej niż jednego rodzaju zdarzenia. Sytuacja CR dzieje się, gdy wystąpienie jednego typu zdarzenia zmienia zdolność do obserwowania interesującego zdarzenia. Miyasaka et al.8 przeprowadził badanie na kohorcie pacjentów, u których zdiagnozowano migotanie przedsionków w latach 1986-2000 w hrabstwie Olmsted w stanie Minnesota w Stanach Zjednoczonych. Głównym rezultatem był początek otępienia. Mediana okresu obserwacji wynosiła 4, 6 lat. Inne rodzaje zdarzeń to wylew i śmierć. Spośród 2837 osób z migotaniem przedsionków, 299 miało demencję, a 1638 zmarło w czasie analizy. Liczby z udarem nie są zgłaszane i są cenzurowane w analizie. Wniosek z badania był taki, że częstość występowania otępienia wśród osób z migotaniem przedsionków jest częsta (10,5% w wieku 5 lat metodą KM). Występowanie udaru mózgu przed otępieniem nie wpływa na obserwację otępienia, a zatem nie jest zdarzeniem CR. Ze względu na argument ignorujemy fakt, że wiele udarów mózgu może powodować demencję. Z drugiej strony, śmierć bez uprzedniej demencji sprawia, że obserwacja demencji jest niemożliwa. Dlatego też zgon bez demencji jest zdarzeniem CR dla punktu końcowego demencji. Również ciężki uraz głowy można uznać za zdarzenie CR, ponieważ zmiany behawioralne pacjenta mogą uniemożliwić rozpoznanie demencji.
bardziej subtelna sytuacja CR występuje w badaniu przeprowadzonym przez Whalley et al.9 o znaczeniu echokardiografii. Ta kohorta 228 pacjentów w podeszłym wieku z objawami przeszła echokardiografię i była obserwowana w przypadku hospitalizacji sercowo-naczyniowej lub zgonu sercowo-naczyniowego. Hipoteza głosiła, że cechy echokardiograficzne przewidują zdarzenia sercowo-naczyniowe. Główny wynik został zdefiniowany jako złożony pomiar obejmujący zgon z przyczyn sercowo-naczyniowych i (lub) hospitalizację. W przypadku tego typu wyników śmierć z przyczyn innych niż choroby sercowo-naczyniowe jest zdarzeniem CR i jako takie pacjent nie jest już narażony na jakiekolwiek z interesujących zdarzeń.
przeprowadzono 3-ramienne, podwójnie zaślepione, randomizowane badanie obejmujące 931 ośrodków i 24 kraje w celu sprawdzenia wpływu walsartanu na walsartan w porównaniu z walsartanem+kaptopryl w porównaniu z samym kaptoprylem (VALIANT)10 na śmiertelność niezależnie od przyczyny. Łącznie 14 703 pacjentów po zawale mięśnia sercowego z dysfunkcją lewej komory i (lub) niewydolnością serca uzyskało wynik 1: 1: 1 W 3 ramionach. Ponieważ każda śmierć była uważana za zdarzenie, ten rodzaj wyniku nie ma CR. Badania potwierdziły hipotezę, że przeżycie w 3 ramionach było inne. Jednakże krwawienie z przewodu pokarmowego zostało zidentyfikowane jako poważne działanie niepożądane we wszystkich 3 grupach. Moukarbel i in.Zbadano czynniki mogące przewidzieć krwawienie z przewodu pokarmowego. Dla tego punktu końcowego śmierć bez krwawienia z przewodu pokarmowego jest wyraźnym CR.
coraz większa liczba badaczy dostrzega obecność CR i potrzebę zastosowania odpowiednich technik. Kohorta 972 pacjentów z ostrym zespołem wieńcowym bez uniesienia odcinka ST w latach 2001-2005 była badana przez Núñez i wsp.12 jednym z celów badań było znalezienie czynników związanych z rehospitalizacją w ostrej niewydolności serca. Wśród badanych czynników były cukrzyca, choroba niedokrwienna serca w wywiadzie, przewlekła niewydolność nerek, historia palenia tytoniu i historia leczenia. Autorzy uznali możliwość wystąpienia CR, takiej jak śmierć przed ponowną hospitalizacją i prawidłowo zastosowali określone techniki, aby wyjaśnić sytuację CR.
13 badano kohortę 1234 pacjentów z objawową chorobą wieńcową, którzy otrzymywali 2 rodzaje leczenia: pomostowanie tętnic wieńcowych (N = 594) lub przezskórna interwencja wieńcowa (n=640). Spośród 301 zgonów zaobserwowanych podczas obserwacji, 42,5% to zgony z serca, a reszta to zgony bez sercowo-naczyniowe. Autorzy prezentują wyniki w zakresie śmiertelności z wszystkich przyczyn, a także w zakresie umieralności z serca i umieralności poza osierdziowej. Zwracają uwagę, że odsetek śmiertelności z wszystkich przyczyn jest sumą odsetka śmiertelności z serca i bez osierdzia prawidłowo oszacowanego z uwzględnieniem CR. Autorzy podkreślają znaczenie analizy każdego z interesujących zdarzeń, a nie łączenia ich w ogólną śmiertelność. Temat ten jest również wyjaśniony na bardziej ogólnym poziomie przez Mella i Jeonga.14
jak można przypuszczać z powyższych przykładów, głównym pytaniem, Kiedy CR są obecne, jest to, czy zignorować CR i cenzurować obserwacje dotyczące CR, czy też uwzględnić CR. Gdy CR są ignorowane, a obserwacje CR są cenzurowane, analiza redukuje się do” zwykłego ” scenariusza czasu do zdarzenia. Ze względu na znajomość tego typu analizy i dostępność oprogramowania, wielu badaczy uciekają się do tego podejścia, jak widać we wcześniejszych przykładach. Jednak nie tylko wśród statystyków jednomyślnie uzgodniono 2, 15, 16, 17, 18, że oszacowanie prawdopodobieństwa zdarzenia w tym przypadku zawyża rzeczywiste prawdopodobieństwo. Kolejnym naturalnym pytaniem jest, czy modelowanie może być wykonywane w tych granicach (ignorowanie/cenzurowanie CR). Jest to bardziej niejednoznaczne i trudniejsze do uchwycenia. Chociaż taka analiza nie może być bez wartości, jej interpretacja jest prawie zawsze obarczona trudnościami. Głównym wymogiem jest to, że zdarzenie CR (którego obserwacje zostały ocenzurowane i zmieszane z prawdziwymi ocenzurowanymi obserwacjami) musi być niezależne od interesującego zdarzenia. W takim przypadku wyniki można interpretować jako efekt kowariant, gdy zdarzenia CR nie istniały. Jednak założenie to zazwyczaj nie może być dokonane i nie może być zweryfikowane lub przetestowane. Podsumowując, za każdym razem, gdy obserwacje CR są cenzurowane, oszacowanie prawdopodobieństwa zdarzenia jest nieprawidłowe, a interpretacja efektu kowariatów nie jest jasna ze względu na brak wiedzy o niezależności między interesującym zdarzeniem a zdarzeniem CR.
gdy analiza jest wykonywana z uwzględnieniem CR (i kodowana wyraźnie z przypadku zainteresowania lub cenzurowania), prawdopodobieństwo jest prawidłowo oszacowane, a modelowanie ma prostą interpretację. Nie ma założenia niezależności, które utrudniałoby interpretację. Obliczony w ten sposób współczynnik kowariaty reprezentuje wpływ tej kowariaty na obserwowane prawdopodobieństwo.
kilku autorów19, 20 próbowało porównać oba podejścia pod względem mocy testów za pomocą symulacji. Badacz musi jednak mieć świadomość, że głównym problemem jest interpretacja wyników. Niezależnie od tego, jak potężne są testy, analiza musi odpowiedzieć na pytanie badania.
szacowanie prawdopodobieństwa zdarzenia
powszechną praktyką jest stosowanie metody KM do szacowania prawdopodobieństwa zdarzenia. Typowy wzór na oszacowanie KM to
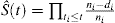
, gdzie t1t2t3ni oznacza liczbę pacjentów zagrożonych w czasie ti, a di oznacza liczbę zdarzeń w czasie ti.
ten wzór można przekształcić za pomocą algebraicznej manipulacji, aby wyrazić prawdopodobieństwo zdarzenia jako:
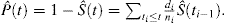
w przypadku CR występują co najmniej 2 rodzaje zdarzeń: zdarzenie będące przedmiotem zainteresowania, identyfikowane z indeksem dolnym e, oraz Zdarzenie ryzyka konkurencyjnego, identyfikowane z indeksem dolnym C. Kalbfleisch i Prentice wprowadzili wzór na prawdopodobieństwo wystąpienia zdarzenia będącego przedmiotem zainteresowania w obecności CR:
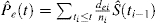
warto zwrócić uwagę na relację pomiędzy (1) i (2). Ponieważ di jest liczbą wszystkich zdarzeń w ti, może być pomyślana jako suma liczby zdarzeń będących przedmiotem zainteresowania dei i liczby zdarzeń CR dci w czasie ti. W związku z tym prawdopodobieństwo dowolnego rodzaju zdarzenia może być rozłożone jako:
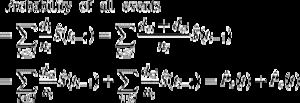
tak więc prawdopodobieństwo wszystkich zdarzeń może być rozłożone w prawdopodobieństwach dla każdego rodzaju zdarzenia.
jeśli do obliczenia prawdopodobieństwa wystąpienia zdarzenia będącego przedmiotem zainteresowania w obecności CR wykorzystuje się 1-KM, to przetrwanie wszystkich zdarzeń we wzorze (2) zastępuje się oszacowaniem KM opartym wyłącznie na zdarzeniach będących przedmiotem zainteresowania. Spowoduje to odchylenie wyników, co zostanie pokazane później. Głównym założeniem stosowania metody KM jest to, że ocenzurowani pacjenci, jeśli będą Obserwowani wystarczająco długo, w końcu doświadczą tego zdarzenia. Jednakże, gdy metoda KM jest stosowana w obecności CR, pacjenci doświadczający rodzajów zdarzeń innych niż zdarzenie będące przedmiotem zainteresowania są zwykle cenzurowani, mimo że nie są już narażeni na ryzyko zdarzenia będącego przedmiotem zainteresowania. Ponadto dla wzoru 1-KM Nie można przeprowadzić rozkładu ładnego widzianego w (3).
w zastosowanych sytuacjach możliwe jest, że istnieje kilka innych rodzajów zdarzeń, które nie są interesujące. W tym przypadku wszystkie mogą być zgrupowane pod parasolem zdarzeń CR.
zostanie pokazane na przykładzie, że stosowanie metody KM nie jest właściwe w obecności CR.
opis przykładu
zestaw danych zebranych w celu zbadania późnych efektów leczenia chłoniaka Hodgkina zostanie wykorzystany do zilustrowania. Głównym wynikiem jest hospitalizacja z powodu choroby serca. Chłoniak Hodgkina jest rodzajem raka, który pojawia się głównie u młodych dorosłych. We wczesnych stadiach jest prawie uleczalny, z 10-letnim całkowitym przeżyciem 70%. Tak więc kohorta tych pacjentów jest idealna do badania długoterminowych skutków ubocznych leczenia. Zastosowany tutaj zbiór danych jest podzbiorem większej kohorty, która zostanie zgłoszona w innym miejscu. Dane są również modyfikowane w celu realizacji naszych celów. Na przykład, dla uproszczenia, trzymaliśmy w danych tylko pacjentów, którzy mieli chemioterapię lub radioterapię, z wyłączeniem tych z leczenia skojarzonego. Aby zwiększyć częstość CR (zgon bez hospitalizacji sercowej), uwzględniliśmy pacjentów wszystkich stadiach. Niektóre obserwacje i daty śmierci zostały przypisane. Ze względu na zmiany, które zostały wprowadzone do danych, nie można wyciągnąć żadnych wniosków klinicznych z tej analizy. Przedstawione dane odnoszą się do 689 zapisów z 93 hospitalizacjami sercowymi i 467 zgonami.
wskaźniki hospitalizacji sercowej i zgonów bez zdarzenia sercowego zostaną obliczone przy użyciu zarówno metody KM (1), jak i cumulative incidence function (CIF) wprowadzonej w tym celu przez Kalbfleischa i Prentice21 (2).
metoda Kaplana-Meiera zastosowana w sytuacji konkurencyjnego ryzyka zawyża rzeczywistą częstość występowania zdarzenia
rycina 1 przedstawia szacunki CIF i 1-KM dla hospitalizacji sercowej w grupie leczonej wyłącznie chemioterapią. Linia przerywana odpowiadająca szacunom 1-KM znajduje się powyżej linii ciągłej reprezentującej szacunki CIF. Można wykazać matematycznie, że 1-KM zawsze przecenia prawdopodobieństwo zdarzenia. Częstym błędem jest to, że szacunki 1-KM są poprawne, jeśli oba wydarzenia są niezależne. Niezależność między zdarzeniami jest zawsze w najlepszym razie wątpliwa, ale nawet gdy dane są symulowane jako niezależne zdarzenia, Istnieje różnica między szacunkami CIF A 1-KM. Wielkość różnicy zależy od liczby zdarzeń, zarówno dla zdarzeń będących przedmiotem zainteresowania, jak i zdarzeń CR. In Miyasaka et al., 8 częstość występowania otępienia w wieku 5 lat metodą KM wynosiła 10,5%. Liczba CR (zgonów) wynosiła około trzech czwartych całkowitej liczby zdarzeń, co sugeruje, że ich szacunki mogą być znacznie większe niż obserwowane.
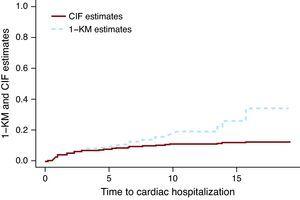
Rysunek 1. Skumulowana funkcja częstości występowania w porównaniu z szacunkami 1-Kaplana-Meiera.. CIF, skumulowana funkcja padania; KM, Kaplan-Meier.
skumulowana funkcja zachorowalności dzieli prawdopodobieństwo jakiegokolwiek zdarzenia (hospitalizacji sercowej lub zgonu) na składowe prawdopodobieństwa
algebraicznie jest to udowodnione w (3). Jednak w celu głębszego zrozumienia, jak to działa, zostanie pokazane graficznie, że od prawdopodobieństwa wszystkich zdarzeń część uczestniczy w CIF dla jednego zdarzenia, a druga do CIF dla drugiego zdarzenia. Rysunek 2A pokazuje prawdopodobieństwo wystąpienia jakiegokolwiek zdarzenia: hospitalizacji sercowej lub zgonu bez hospitalizacji sercowej. Rysunek 2B zawiera tylko krzywą między 10.7 a 10.85 lat, tak, że kroki są widoczne. Na każdym kroku znajduje się okrąg. Otwarte kręgi pojawiają się na stopniach, w których zaobserwowano śmierć, podczas gdy kręgi stałe znajdują się na stopniach, w których wystąpiła hospitalizacja sercowa. Kroki z kręgami stałymi uczestniczą w CIF dla hospitalizacji sercowej w panelu C, a te z otwartymi kręgami uczestniczą w krzywej śmierci na rysunku 2D. Tak więc każdy krok przyczyni się do prawdopodobieństwa zdarzenia, które go powoduje. W ten sposób, w dowolnym momencie prawdopodobieństwo wszystkich zdarzeń jest sumą prawdopodobieństwa zdarzenia będącego przedmiotem zainteresowania i prawdopodobieństwa CR. Należy zauważyć, że Ostatnie 3 panele (rysunek 2B-D) pokazują to samo okno czasu i mają tę samą długość dla osi y, tak że można porównać rozmiar kroków między nimi. Tabela 1 przedstawia te prawdopodobieństwa po 1, 2, 3, 4 i 5 latach.
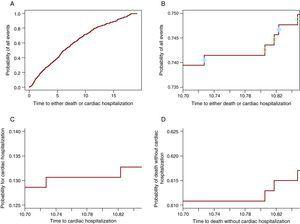
Rysunek 2. Podział prawdopodobieństwa wszystkich zdarzeń na prawdopodobieństwa składowe. A. prawdopodobieństwo hospitalizacji serca lub śmierci. B. prawdopodobieństwo hospitalizacji serca lub śmierci tylko przez okno czasu 10,70-10,85 lat. Kręgi stałe wskazują na hospitalizację serca, a kręgi otwarte oznaczają zgony bez hospitalizacji serca. C. prawdopodobieństwo hospitalizacji serca w oknie czasu 10,70 -10,85 lat. D. prawdopodobieństwo zgonu bez hospitalizacji sercowej w oknie czasu 10.70-10.85.
Tabela 1. Prawdopodobieństwo dla dowolnego zdarzenia jest sumą prawdopodobieństw składowych.
| rok zgłoszenia | prawdopodobieństwo hospitalizacji sercowej | prawdopodobieństwo zgonu | prawdopodobieństwo hospitalizacji sercowej lub zgonu |
| 1 | 0.038 | 0.054 | 0.092 |
| 2 | 0.054 | 0.139 | 0.193 |
| 3 | 0.072 | 0.193 | 0.265 |
| 4 | 0.076 | 0.25 | 0.327 |
| 5 | 0.087 | 0.305 | 0.392 |
ponieważ 1-KM przecenia prawdopodobieństwo zdarzenia, gdybyśmy spróbowali dodać 1-KM oszacowania hospitalizacji sercowej do 1-KM zgonu, uzyskalibyśmy znacznie wyższy wskaźnik niż prawdopodobieństwo jakiegokolwiek zdarzenia. W niektórych przypadkach uzyskana liczba jest nawet większa niż 1, co dowodzi, że w obecności CR szacunki 1-KM nie są nawet prawdopodobieństwami.
czy metoda Cumulative Incidence Function rzeczywiście szacuje prawidłowe prawdopodobieństwo zdarzenia?
w tym celu symulowano zbiór 500 rekordów tak, że nie ma cenzury przed 5 latami i istnieją 2 typy zdarzeń: typ 1 i 2. Tabela 2 pokazuje dla każdego rodzaju zdarzenia liczbę obserwowaną do tego momentu w czasie, szybkość surowa i oszacowanie CIF, które są dokładnie równe. Równość zachodzi tylko wtedy, gdy nie ma ocenzurowanych obserwacji do tego momentu. W obecności ocenzurowanych obserwacji w raportowanych latach równość nie utrzymuje się, a prawidłowym sposobem oszacowania prawdopodobieństwa jest CIF, A nie stawka surowa.
Tabela 2. Prawdopodobieństwo wystąpienia dwóch rodzajów zdarzeń, gdy nie ma ocenzurowanych obserwacji do 5 lat.
CIF, funkcja skumulowanej częstości występowania.
podsumowując, aby obliczyć prawdopodobieństwo zdarzenia w obecności CR, należy użyć metody wprowadzonej przez Kalbfleischa i Prentice ’ a, zwyczajowo nazywanej krzywą skumulowanej częstości występowania.
modelowanie
ważnym aspektem w analizie jest testowanie związku między kowariatą a interesującym zdarzeniem, samodzielnie lub dostosowując się do innych czynników. W przypadku braku CR jest to rutynowo realizowane za pomocą modelu proporcjonalnego ryzyka Coxa (COX PH).
w obecności CR model PH Coxa nie ma prostej interpretacji. Jeśli czas do 2 rodzajów zdarzeń można uznać za niezależny, To wyniki można interpretować jako pokazujące efekt w sytuacji, gdy CR nie istnieje. Jednak założenie niezależności rzadko może być wykonane lub przetestowane, a zatem wyniki z modelu PH Coxa zwykle nie są interpretowalne.
Model Fine I Gray
Fine I Gray6 (F&G) zmodyfikowały Model PH Coxa, aby umożliwić obecność CR. Zmiana techniczna polega na utrzymywaniu obserwacji CR w zestawie ryzyka ze zmniejszającą się wagą. W ten sposób Metoda F& G modeluje zagrożenia subdystrybucji. Efekt oszacowany przy użyciu modelu F& G pokazuje aktualne i rzeczywiste różnice między grupami poddystrybucyjnymi pod względem współczynników zagrożeń subdystrybucyjnych. Założenie proporcjonalności zagrożeń jest nadal wymogiem, ale oczywiście odnosi się do zagrożeń subdystrybucyjnych. Model F& G może pomieścić współczynniki zależne od czasu do modelowania nieproporcjonalności zagrożeń. Model ten może być stosowany zarówno w przypadku zainteresowania (hospitalizacja sercowa), jak i CR (zgon).
modele PH Coxa i F&G zostały zastosowane do zestawu danych dotyczących chłoniaka Hodgkina w celu przetestowania opcji leczenia chemioterapią a radioterapią. W tym przykładzie (Tabela 3) wyniki z modeli Ph Coxa i F& G znacznie się różnią (pierwsze 2 rzędy). Jak wspomniano powyżej, wyniki COX PH nie są interpretowalne i nie mogą być wykorzystane. Drugi rząd pokazuje więcej hospitalizacji sercowych w grupie radioterapii, a trzeci rząd pokazuje więcej zgonów w grupie chemioterapii. Rysunek 3 przedstawia te wyniki graficznie. Możliwe, że samą chemioterapię podawano pacjentom z bardziej zaawansowaną chorobą, a ci pacjenci byli również bardziej narażeni na śmierć z powodu raka. Z drugiej strony samo naświetlanie było prawdopodobnie podawane pacjentom we wczesnym stadium, którzy żyli dłużej po rozpoznaniu chłoniaka Hodgkina. Pacjenci ci mieli większe szanse na wystąpienie późnych działań niepożądanych, takich jak choroba serca.
Tabela 3. Efekt leczenia przy zastosowaniu proporcjonalnych zagrożeń Cox oraz modeli cienkich i szarych.
CI, przedział ufności; PH Coxa, model ryzyka proporcjonalnego Coxa; F& G, Model drobnego i szarego; HR, współczynnik ryzyka.
współczynniki ryzyka wskazują na wzrost ryzyka dla grupy naświetlanej w porównaniu do grupy otrzymującej chemioterapię.
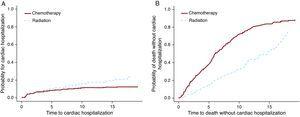
Rysunek 3. Efekt leczenia hospitalizacji sercowej i śmierci.
jak widać na tym przykładzie, interpretacja wyników jest dziełem współpracy między statystykiem a klinicystą, który ma gruntowną wiedzę na temat choroby.
obecność CR komplikuje zarówno analizę, jak i interpretację danych. Aby czytelnik mógł prawidłowo zinterpretować wyniki, autorzy muszą zawrzeć szczegóły na temat obserwowanych zdarzeń, nawet jeśli na pierwszy rzut oka mogą one nie wydawać się ważne. Dlatego, gdy punkt końcowy jest obserwowany w czasie, autorzy muszą uwzględnić zdarzenie będące przedmiotem zainteresowania, czy istnieje możliwość wystąpienia CR, ilu pacjentów doświadcza któregokolwiek z tych rodzajów zdarzeń oraz czas trwania obserwacji. W przypadku CR jest pouczające, aby uwzględnić analizę dla zdarzenia będącego przedmiotem zainteresowania, jak również analizę dla CR, ponieważ uzupełniają się one wzajemnie i mogą pomóc w interpretacji wyników.
podejście logistyczne
Załóżmy najpierw, że jesteśmy w ramach no CR. Gdy oczekuje się, że wynik nastąpi w krótkim odstępie czasu (np. 1 rok), narzędziem z wyboru dla wielu badaczy jest regresja logistyczna. Jest to właściwe, jeśli każda osoba w kohorcie ma minimalny okres obserwacji, w tym przypadku 1 rok. W rzeczywistości szacunki dotyczące śmiertelności na 1 rok będą pokrywać się z szacunkami na 1 KM. Czasowy punkt odcięcia musi być taki sam dla każdego osobnika w kohorcie. W związku z tym, jeśli wynikiem zainteresowania jest śmiertelność roczna, a 1 osoba w kohorcie umiera po 1 roku i 2 dniach, osobę tę należy uznać za „brak zdarzenia po 1 roku.”Może to zmniejszyć liczbę zdarzeń, co przekłada się na mniej niż idealną analizę, gdy wiele obserwowanych zdarzeń występuje po punkcie odcięcia.
te same podstawowe zasady obowiązują w przypadku CR. Wszystkie osoby w kohorcie muszą mieć minimalny okres obserwacji wybrany jako punkt graniczny, a ten punkt graniczny musi mieć zastosowanie do wszystkich osób w kohorcie. Współczynniki i wartości p ogólnie dadzą ten sam komunikat, ale nie będą dokładnie takie same dla regresji logistycznej w porównaniu do modelu F& G. Po pierwsze, w regresji logistycznej współczynnik reprezentuje log stosunku szans, podczas gdy w modelu F& G jest to log stosunku poddystrybucji zagrożeń. Ponadto w analizie logistycznej nie wszystkie zdarzenia są wykorzystywane i oczywiście używany jest inny model.
obliczanie mocy
gdy miarą jest czas do zdarzenia, obliczanie mocy ma dwa etapy. Pierwszym krokiem jest obliczenie liczby zdarzeń potrzebnych do wykrycia określonego rozmiaru efektu. Następnie obliczana jest liczba pacjentów potrzebnych do zaobserwowania tej liczby zdarzeń. W poprzednich sekcjach podkreślono, że w przypadku obecności CR nie jest możliwe zaobserwowanie wszystkich interesujących zdarzeń ze względu na występowanie CR. Ponieważ liczba zdarzeń ma kluczowe znaczenie przy obliczaniu mocy, należy zachować szczególną ostrożność, aby uwzględnić CR. Jeśli CR nie zostaną uwzględnione, badanie będzie niedostateczne, a zatem prawdopodobnie nieudane (i prawdopodobnie nieetyczne).
oprogramowanie
oprogramowanie open source R na stronie Cran (the Comprehensive R Archive Network) (http://cran.r-project.org/) oferuje pakiet (cmprsk) zaimplementowany przez Dr. Robert Gray zawierający niezbędne narzędzia do pełnej analizy księgowej dla CR. W ten sposób można uzyskać zaobserwowane wykresy prawdopodobieństwa dla zdarzenia będącego przedmiotem zainteresowania i wartość p na podstawie testu Graya, który jest zmodyfikowanym testem logrank dla sytuacji CR. W pakiecie znajduje się również funkcja do modelowania przy użyciu podejścia F&G. Luca Scruca ulepszył dostarczanie danych wyjściowych funkcji modelowania w celu łatwiejszego odczytu poprzez włączenie do pakietu funkcji typu podsumowania. Model ma możliwość sprawdzenia proporcjonalności zagrożeń, można też uwzględnić współczynniki zależne od czasu. Kod nie może pomieścić danych o skracaniu lewej strony ani danych klastra. Lewe obcięcie byłoby przydatne do analizy wielokrotnych / nawracających zdarzeń na pacjenta lub do analizy kohorty przypadków. Opracowano kod dla badań kohortowych przypadków (Pintilie et al.23) i można uzyskać od autorów. Zhou et al.24 rozszerzył model F& G, aby pomieścić dane stratyfikowane, a także będzie miał wersję dla danych klastrowych. W tym momencie kod można uzyskać od autorów w obu przypadkach, ale jest prawdopodobne, że zostanie on przedłożony CRAN.
STATA 11 niedawno wdrożył model F & G. Trzeba mieć świadomość, że wykresy uzyskane za pomocą STATA są predykcyjne, a nie obserwowane wykresy prawdopodobieństwa. Istnieją dwa zastrzeżenia, gdy stosowane są przewidywane krzywe: a) linie zawsze będą wyglądać tak, jakby proporcjonalność zagrożeń była spełniona, a b) liczba kroków w każdej krzywej będzie większa niż liczba zdarzeń w każdej podgrupie, sprawiając wrażenie, że zdarzeń jest więcej niż w rzeczywistości.
wnioski
dostępność dużych zbiorów danych z kompletnym monitorowaniem dla kilku punktów końcowych stale rośnie. Istnieje również rosnąca potrzeba analiz, które dotyczą precyzyjnego punktu końcowego, takiego jak śmierć z powodu niewydolności serca lub kontrola choroby lub kontrola choroby miejscowej. Wszystkie te punkty końcowe mogą potencjalnie mieć CR. W związku z tym istotne jest, aby CR był brany pod uwagę od etapu projektowania do interpretacji wyników. Podczas gdy model PH Coxa może mieć ograniczoną wartość, gdy rozważa się niezależność, szacunki KM nie są poprawne i nie mogą być interpretowane. W związku z tym należy zastosować określone techniki, takie jak modele CIF i F&G, dostępne w R i częściowo w STATA.
konflikt interesów
Brak ogłoszeń.