introdução
riscos concorrentes (CR) tem sido reconhecida como um caso especial de Análise tempo-A-evento desde o século XVIII. Ocasionalmente, trabalhos na área estatística ou matemática foram publicados incorporando novos desenvolvimentos, incluindo a monografia de David e Moeschberger.1 à medida que os dados se tornaram mais extensos, claros e precisos em relação aos diferentes tipos de resultados, o CR ressurgiu como um tipo crucial de análise dentro da análise tempo-A-Evento, necessário para uma melhor compreensão de uma doença. A conexão entre os resultados matemáticos e o campo aplicado precisava ser feita. Vários autores contribuíram para a compreensão das situações CR.2, 3 outros autores aperfeiçoaram e desenvolveram técnicas e, em alguns casos, disponibilizaram código de computador pronto a usar para estatísticas aplicadas.4, 5, 6
Introdução à análise TEMPO-A-evento
em muitos estudos o resultado é observado longitudinalmente. Desta forma, cada sujeito na coorte é observado por um período de tempo até que o evento ocorra. Por exemplo, o evento de interesse pode ser Morte, ataque cardíaco, ou recorrência de câncer. Os objetivos do estudo podem ser estimar a probabilidade da ocorrência do evento ou sua associação com covariados de interesse como tratamento ou características do sujeito. A análise estatística utilizada é chamada Análise tempo-A-evento ou às vezes análise de sobrevivência. O método mais comum para estimar a probabilidade de um evento é uma abordagem não paramétrica habitualmente chamada de método Kaplan-Meier7 (KM) ou método de limite de produto. A principal suposição da estimativa do KM para a sobrevivência é que as observações censuradas experimentarão o evento se forem seguidas o tempo suficiente.
para o resto deste artigo, as probabilidades para o evento serão dadas em vez da probabilidade de livre-evento. Por exemplo, em vez de probabilidade de sobrevivência, a probabilidade de morte será apresentada, que pode ser estimada usando o complemento do estimador KM: 1-KM.
Introdução A riscos concorrentes
não é raro um participante num estudo experimentar mais do que um tipo de Evento. Uma situação CR acontece quando a ocorrência de um tipo de Evento muda a capacidade de observar o evento de interesse. Miyasaka et al.8 conduziu um estudo sobre uma coorte comunitária de doentes diagnosticados com fibrilhação auricular entre 1986 e 2000 no Condado de Olmsted, Minnesota, Estados Unidos. O principal resultado foi o início da demência. O seguimento mediano foi de 4, 6 anos. Outros tipos de eventos foram acidente vascular cerebral e morte. Dos 2837 indivíduos com fibrilhação auricular, 299 tinham demência e 1638 morreram na altura da análise. Os números com acidente vascular cerebral não são relatados e são censurados na análise. A conclusão do estudo foi que a incidência de demência entre os indivíduos com fibrilhação auricular é comum (10, 5% aos 5 anos usando o método KM). A ocorrência de acidente vascular cerebral antes da demência não afecta a observação da demência, pelo que não é um acontecimento CR. Por razões de argumento, ignoramos o facto de que múltiplos derrames podem causar demência. Por outro lado, uma morte sem demência prévia torna a observação da demência impossível. Portanto, uma morte sem demência é um evento CR para o endpoint da demência. Também uma lesão grave na cabeça pode ser considerado um evento CR, uma vez que as alterações comportamentais do paciente pode tornar o diagnóstico de demência impossível.
uma situação CR mais sutil ocorre no estudo conduzido por Whalley et al.9 da importância da ecocardiografia. Este grupo de 228 doentes idosos sintomáticos foi submetido a ecocardiografia e foi seguido para hospitalização cardiovascular ou morte cardiovascular. A hipótese era que a ecocardiografia apresenta previsão de eventos cardiovasculares. O resultado principal foi definido como a medida composta incluindo morte cardiovascular e/ou hospitalização. Para este tipo de resultado, uma morte devido a outras causas que não doenças cardiovasculares é um evento CR e, como tal, um paciente não está mais em risco de ter qualquer um dos eventos de interesse.
foi realizado um ensaio aleatorizado, em dupla ocultação, com 3 braços, abrangendo 931 centros e 24 países para testar o efeito de valsartan vs valsartan+captopril vs captopril isoladamente (VALIANT)10 na mortalidade por todas as causas. No total, 14 703 doentes pós-enfarte do miocárdio com disfunção ventrículo esquerdo e/ou insuficiência cardíaca aumentaram 1:1:1 nos 3 braços. Uma vez que qualquer morte foi considerada um evento, este tipo de resultado não tem CR. O estudo apoiou a hipótese de que a sobrevivência nos 3 braços era diferente. Contudo, a hemorragia gastrointestinal (GI) foi identificada como um efeito secundário grave em todos os 3 braços. Moukarbel et al.Estudou os possíveis factores que podiam prever a hemorragia gastrointestinal. Para este parâmetro, a morte sem hemorragia gastrointestinal é uma CR clara.
um número crescente de pesquisadores reconhecem a presença de CR e a necessidade de técnicas adequadas a serem aplicadas. Uma coorte de 972 doentes com síndrome coronária aguda sem elevação do segmento ST entre 2001 e 2005 foi estudada por Núñez et al.Um dos objectivos do estudo foi encontrar factores associados à hospitalização para insuficiência cardíaca aguda. Entre os factores estudados estavam a diabetes, antecedentes de doença cardíaca isquémica, insuficiência renal crónica, história de tabagismo e história de tratamento. Os autores reconheceram a possibilidade de CR como a morte antes da hospitalização e aplicaram corretamente técnicas específicas para explicar a situação CR.
Melberg et al.Estudou uma coorte de 1234 doentes com doença arterial coronária sintomática que receberam 2 tipos de tratamentos: enxerto de bypass da artéria coronária (n=594) ou intervenção coronária percutânea (n=640). Das 301 mortes observadas durante o seguimento, 42, 5% foram mortes cardíacas e as restantes foram mortes não cardiacas. Os autores apresentam resultados para a mortalidade por todas as causas, bem como para a mortalidade Cardíaca e mortalidade não-cardiaca. Eles apontam que a porcentagem de mortalidade por todas as causas é a soma da porcentagem de mortalidade Cardíaca e não cardiaca corretamente estimada tendo em conta a CR. Os autores enfatizam a importância de analisar cada um dos eventos de interesse ao invés de combiná-los em uma mortalidade global. Este tópico também é exposto a um nível mais geral por Mell e Jeong.14
como se pode inferir dos exemplos acima, a principal questão quando CR está presente é se deve ignorar o CR e censurar as observações que envolvem CR ou prestar contas de CR. Quando o CR é ignorado e as observações do CR são censuradas, a análise reduz-se a um cenário “usual” de tempo para evento. Devido à familiaridade deste tipo de análise e à disponibilidade de software, muitos pesquisadores recorrem a esta abordagem, como visto nos exemplos anteriores. No entanto, é unanimemente acordado não só entre os estatísticos2, 15, 16, 17, 18 que a estimativa da probabilidade do evento neste caso sobrestima a probabilidade real. A próxima questão natural é se a modelagem pode ser realizada dentro desses limites (ignorando/censurando CR). Isto é mais ambíguo e mais difícil de entender. Embora tal análise possa não ser isenta de valor, a sua interpretação está quase sempre repleta de dificuldades. O principal requisito é que o evento CR (cujas observações foram censuradas e misturadas com as verdadeiras observações censuradas) precisa ser independente do evento de interesse. Se este for o caso, então os resultados podem ser interpretados como o efeito de covariatas quando os eventos CR não existiam. No entanto, este pressuposto não pode normalmente ser feito e não pode ser verificado ou testado. Em conclusão, cada vez que as observações CR são censuradas, a estimativa da probabilidade do evento é incorreta e a interpretação do efeito das covariadas não é clara devido à falta de Conhecimento da independência entre o evento de interesse e evento CR.
Quando a análise é realizada de contabilidade para CR (e codificados de forma distinta do evento de interesse ou de censura), então a probabilidade é estimado corretamente e a modelagem de uma simples interpretação. Não há suposição de independência para dificultar a interpretação. O coeficiente de um covariato assim estimado representa o efeito desse covariato nas probabilidades observadas.
vários autores 19, 20 tentaram comparar as duas abordagens em termos do poder dos testes usando simulações. No entanto, o pesquisador precisa estar ciente de que o principal problema está na interpretação dos resultados. Independentemente de quão poderosos são os testes, a análise precisa responder à questão do estudo.
estimar a probabilidade de um evento
é prática comum aplicar o método KM para estimar a probabilidade de um evento. A fórmula típica para o KM estimativa é
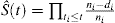
, onde t1t2t3ni representa o número de pacientes em risco no instante ti e di é o número de eventos no tempo ti.
Esta fórmula pode ser transformada através de manipulação algébrica para expressar a probabilidade do evento:
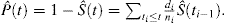
Na presença de CR, existem pelo menos 2 tipos de eventos: evento de interesse, identificados com o índice e, e os concorrentes evento de risco, identificados com o subscrito c. Kalbfleisch e Prentice introduzida a fórmula para a probabilidade de um evento de interesse na presença de CR:
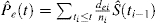
é interessante notar a relação entre (1) e (2). Uma vez que di é o número de todos os eventos na ti, ele pode ser concebido como a soma do número de eventos de interesse dei e o número de eventos CR dci no momento ti. Como tal, a probabilidade de qualquer tipo de evento pode ser decomposta como:
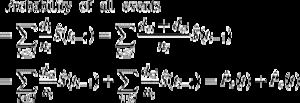
Assim, a probabilidade de todos os eventos pode ser decomposto na soma das probabilidades para cada tipo de evento.
Se 1 KM é utilizado para calcular a probabilidade de um evento de interesse na presença de CR, a sobrevivência de todos os eventos na fórmula (2) é substituído pelo KM estimativa com base em eventos de interesse apenas. Isto irá influenciar os resultados, como será mostrado mais tarde. A principal suposição para o uso do método KM é que os pacientes censurados, se seguidos o tempo suficiente, eventualmente experimentarão o evento. No entanto, quando o método KM é usado na presença de CR, os pacientes que experimentam outros tipos de eventos que não o evento de interesse são geralmente censurados, mesmo que não estejam mais em risco para o evento de interesse. Além disso, a decomposição de nice vista em (3) não pode ser realizada para a fórmula de 1 KM.
em situações Aplicadas é possível que existam vários outros tipos de eventos que não são de interesse. Neste caso, todos podem ser agrupados sob a égide de eventos CR.
será mostrado através de um exemplo que o uso do método KM não é apropriado na presença de CR.
Descrição do exemplo
um conjunto de dados recolhidos para estudar os efeitos tardios do tratamento do linfoma de Hodgkin será utilizado para ilustração. O principal resultado é a hospitalização por doença cardíaca. O linfoma de Hodgkin é um tipo de câncer que aparece principalmente em adultos jovens. Em seus estágios iniciais é quase curável, com uma sobrevivência global de 10 anos de 70%. Assim, uma coorte destes doentes é ideal para estudar os efeitos secundários a longo prazo do tratamento. O conjunto de dados aqui utilizado é um subconjunto de uma coorte maior que será reportado noutro local. Os dados também são modificados para servir os nossos propósitos. Por exemplo, para simplificar, mantivemos nos dados apenas pacientes que tiveram quimioterapia ou radiação, excluindo aqueles com tratamento combinado. Para aumentar a taxa de CR (morte sem hospitalização cardíaca), incluímos pacientes de todas as fases. Algumas datas de Seguimento e morte foram imputadas. Devido às modificações que foram feitas aos dados, nenhuma conclusão clínica pode ser retirada desta análise. Os dados aqui apresentados referenciam 689 registros com 93 hospitalizações cardíacas e 467 mortes.
as taxas de hospitalização Cardíaca e de morte sem evento cardíaco serão calculadas utilizando o método KM (1) e a função de incidência cumulativa (CIF) introduzida por Kalbfleisch e Prentice21 para este efeito (2).
o método Kaplan-Meier aplicado a uma situação de risco concorrente Sobrestima a taxa real do evento
a Figura 1 apresenta as estimativas CIF e 1 KM para a hospitalização cardíaca do grupo tratado apenas com quimioterapia. A linha quebrada correspondente às estimativas de 1 KM situa-se acima da linha sólida que representa as estimativas CIF. Pode ser mostrado matematicamente que 1 KM sempre sobrestima a probabilidade do evento. Um equívoco comum é que as estimativas de 1 KM estão corretas se os dois eventos são independentes. A independência entre Eventos é sempre questionável na melhor das hipóteses, mas mesmo quando os dados são simulados como eventos independentes, a diferença entre as estimativas CIF e os 1 KM existe. O tamanho da diferença depende do número de eventos, tanto para eventos de interesse quanto para os eventos CR. In Miyasaka et al.,8 a incidência de demência aos 5 anos de idade utilizando o método KM foi de 10, 5%. O número de CR (mortes) foi de cerca de três quartos do número total de eventos, o que sugere que sua estimativa pode ser muito maior do que o observado.
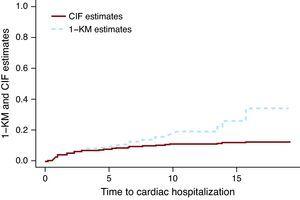
Figura 1. Função de incidência cumulativa vs estimativas de 1-Kaplan-Meier.. CIF, função de incidência cumulativa; KM, Kaplan-Meier.
a função de incidência cumulativa divide a probabilidade de qualquer evento (hospitalização cardíaca ou morte) nas probabilidades constituintes
algebricamente isto é provado em (3). No entanto, para uma compreensão mais profunda de como funciona, será mostrado graficamente que a partir da probabilidade de todos os Eventos uma parte participa do CIF para um evento e o outro para o CIF para o outro evento. A figura 2A mostra a probabilidade de qualquer evento: hospitalização cardíaca ou morte sem hospitalização cardíaca. A figura 2B contém apenas a curva entre 10,7 e 10.85 anos, de modo que os passos sejam visíveis. Em cada passo há um círculo. Os círculos abertos aparecem nos degraus em que foi observada uma morte enquanto os círculos sólidos estão nos degraus em que ocorreu uma hospitalização cardíaca. Os passos com círculos sólidos participam no CIF para a hospitalização cardíaca no painel C e os com círculos abertos participam da curva para a morte na figura 2D. assim, cada passo contribuirá para a probabilidade do evento que o causa. Desta forma, em qualquer momento a probabilidade de todos os Eventos é a soma da probabilidade do evento de interesse e da probabilidade de CR. Note – se que os últimos 3 painéis (figura 2B-D) mostram a mesma janela de tempo e têm o mesmo comprimento para o eixo y, de modo que o tamanho dos degraus pode ser comparado entre eles. A tabela 1 mostra essas probabilidades em 1, 2, 3, 4 e 5 anos.
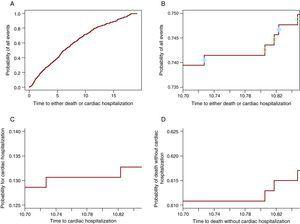
Figura 2. A partição da probabilidade de todos os eventos nas probabilidades constituintes. A. a probabilidade de hospitalização cardíaca ou morte. B. A probabilidade de hospitalização cardíaca ou morte apenas pela janela de tempo 10.70 – 10.85 anos. Os círculos sólidos indicam a hospitalização Cardíaca e os círculos abertos representam Mortes sem hospitalização cardíaca. C. A probabilidade de hospitalização cardíaca na janela de tempo 10.70-10.85 anos. D. A probabilidade de morte sem hospitalização cardíaca na janela de tempo 10.70-10.85.
Quadro 1. A probabilidade para qualquer evento é a soma das probabilidades constituintes.
| Ano de relatórios | Probabilidade de cardíaco, hospitalização | Probabilidade de morte | Probabilidade de um cardíaco, hospitalização ou morte |
| 1 | 0.038 | 0.054 | 0.092 |
| 2 | 0.054 | 0.139 | 0.193 |
| 3 | 0.072 | 0.193 | 0.265 |
| 4 | 0.076 | 0.25 | 0.327 |
| 5 | 0.087 | 0.305 | 0.392 |
Porque a 1 KM superestima a probabilidade de um evento, se nós tentamos adicionar a 1 KM de estimativas cardíaca de internação para a de 1 KM para a morte, poderemos obter uma taxa muito mais elevada do que a probabilidade de qualquer evento. Em alguns casos, o número obtido é ainda maior que 1, o que prova que, na presença de CR, estimativas de 1 KM nem sequer são probabilidades.
o método da função de incidência cumulativa realmente estima a probabilidade correta do evento?
para este efeito, um conjunto de dados de 500 registos foi simulado de modo a que não haja censura antes de 5 anos e existam 2 tipos de eventos: Tipo 1 e 2. O quadro 2 mostra, para cada tipo de evento, o número observado até esse ponto no tempo, a taxa bruta e a estimativa CIF, que são exatamente iguais. A igualdade só acontece quando não há observações censuradas até esse momento. Na presença de observações censuradas dentro dos anos relatados a igualdade não se mantém e a maneira correta de estimar a probabilidade é o CIF e não a taxa bruta.
Quadro 2. A probabilidade dos dois tipos de Evento quando não há observações censuradas até 5 anos.
CIF, função de incidência cumulativa.
em conclusão, para calcular a probabilidade de Evento na presença de CR um tem que usar o método introduzido por Kalbfleisch e Prentice, habitualmente chamado de curva de incidência cumulativa.
modelagem
um aspecto importante em uma análise é testar a associação entre uma covariação e o evento de interesse, quer sozinho ou ajustando para outros fatores. Na ausência de CR isto é rotineiramente realizado usando o modelo Cox proportional hazards (Cox PH).22
na presença de CR, o modelo Cox PH não tem uma interpretação simples. Se o tempo para os 2 tipos de eventos Pode ser considerado independente, então os resultados podem ser interpretados como mostrando o efeito na situação em que CR não existe. However, the assumption of independence can rarely be made or tested and thus the results from Cox PH model are usually not interpretable.
Fine and Gray Model
Fine and Gray6 (F&G) modified the Cox PH model to allow for the presence of CR. A alteração técnica consiste em manter as observações do CR no risco fixado com um peso reduzido. Desta forma, o método F&G modela os perigos de subdistribuição. O efeito estimado utilizando o modelo F &G mostra as diferenças actuais e reais entre os grupos de tratamento em termos de rácios de perigos de subdistribução. O pressuposto da proporcionalidade dos perigos continua a ser um requisito, mas é claro que se refere aos perigos de subdistribuição. O modelo F & G pode acomodar coeficientes dependentes do tempo para modelar a não-proporcionalidade dos perigos. Este modelo pode ser aplicado tanto ao evento de interesse (hospitalização cardíaca) ou a CR (morte).Os modelos Cox PH E F & G foram aplicados ao conjunto de dados do linfoma de Hodgkin para testar a opção de tratamento da quimioterapia vs radiação. Para este exemplo (Quadro 3), os resultados dos modelos Cox PH e F&G diferem substancialmente (primeiras 2 linhas). Como mencionado acima, os resultados do pH Cox não são interpretáveis e não podem ser usados. A segunda linha mostra que há mais hospitalizações cardíacas entre o grupo de radiação e a terceira linha mostra mais mortes entre o grupo de quimioterapia. A figura 3 mostra estes resultados graficamente. É possível que a quimioterapia, por si só, tenha sido administrada a doentes com doença mais avançada, sendo que estes doentes também tinham maior probabilidade de morrer de cancro. Por outro lado, a radiação por si só foi provavelmente dada a doentes numa fase inicial que viveram mais tempo após o diagnóstico do linfoma de Hodgkin. Estes doentes tiveram mais hipóteses de desenvolver efeitos secundários tardios, como doença cardíaca.
Quadro 3. O efeito do tratamento quando os riscos proporcionais Cox e modelos finos e cinzentos são empregados.
IC, intervalo de confiança; Cox PH, modelo de perigos proporcionais à Cox; F&G, modelo fino e cinzento; HR, taxa de risco.
as razões de perigo mostram o aumento dos perigos para o grupo de radiação em comparação com o grupo de quimioterapia.
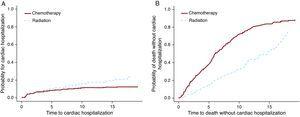
Figura 3. O efeito do tratamento para hospitalização Cardíaca e para a morte.
como pode ser visto a partir deste exemplo, a interpretação dos resultados é um trabalho de colaboração entre o estatístico e o clínico que tem um conhecimento profundo da doença.
a presença de CR complica tanto a análise como a interpretação dos dados. Para permitir que o leitor interprete corretamente os resultados, os autores precisam incluir detalhes sobre os eventos observados, embora possam não parecer importantes à primeira vista. Portanto, quando o ponto final é observado ao longo do tempo, os autores precisam incluir o evento de interesse, se existe a possibilidade de CR, como muitos pacientes experimentam qualquer um destes tipos de eventos, e a duração do follow-up. Na presença de CR é informativo incluir a análise para o evento de interesse, bem como a análise para CR, uma vez que eles se complementam e podem ajudar a interpretar os resultados.
a abordagem logística
vamos supor primeiro que estamos no quadro de nenhuma CR. Quando se espera que o resultado ocorra dentro de um curto intervalo (por exemplo, 1 ano), a ferramenta de escolha para muitos pesquisadores é a regressão logística. Isto é apropriado se cada indivíduo da coorte tiver o acompanhamento mínimo, neste caso um ano. De facto, a estimativa da mortalidade de 1 ano coincidirá com a estimativa de 1 KM. O ponto de corte temporal precisa ser o mesmo para cada indivíduo na coorte. Portanto, se o resultado do interesse é mortalidade de 1 ano e 1 indivíduo na coorte morre em 1 ano e 2 dias, essa pessoa deve ser considerada como “nenhum evento em 1 ano.”Isso pode reduzir o número de eventos, o que se traduz em uma análise menos do que ideal quando muitos eventos observados ocorrem após o ponto de corte.
as mesmas regras básicas se aplicam quando CR está presente. Todos os indivíduos da coorte devem ter o acompanhamento mínimo escolhido como ponto-limite de tempo, e esse ponto-limite deve aplicar-se a todos na coorte. Os coeficientes e valores-p darão, em geral, a mesma mensagem, mas não serão exatamente os mesmos para a regressão logística em comparação com o modelo F&G. Em primeiro lugar, na regressão logística, o coeficiente representa o log da razão de probabilidades, enquanto no modelo F&G é o log da razão das subdistribuições de perigos. Além disso, na análise logística nem todos os eventos são usados e, claro, um modelo diferente é usado.
cálculo de potência
quando a medida é de tempo para evento, o cálculo de potência tem duas fases. O primeiro passo é calcular o número de eventos necessários para detectar um tamanho de efeito específico. Em seguida, o número de pacientes necessários para observar esse número de Eventos é calculado. Foi enfatizado nas seções anteriores que quando CR está presente não é possível observar todos os eventos de interesse devido à ocorrência de CR. Uma vez que o número de Eventos é central no cálculo do poder, é necessário ter mais cuidado para garantir que o CR é tido em conta. Se o CR não for considerado, então o estudo será mal sucedido e, portanto, provavelmente mal sucedido (e possivelmente não ético).
SOFTWARE
the open source R software on CRAN (the Comprehensive R Archive Network) site (http://cran.r-project.org/) offers a package (cmprsk) implemented by Dr. Robert Gray containing the necessary tools for a complete analysis accounting for CR. Assim, pode-se obter gráficos de probabilidade observados para o evento de interesse e um valor p baseado no teste de Gray, que é um teste logrank modificado para a situação CR. Dentro do pacote há também uma função para modelagem usando a abordagem F &G. Luca Scruca aprimorou a entrega de saída da função de modelagem para uma leitura mais fácil, incorporando no pacote uma função de tipo de resumo. O modelo tem a possibilidade de verificar a proporcionalidade dos perigos, e os termos para coeficientes dependentes do tempo podem ser incluídos. O código não pode acomodar dados de truncamento ou cluster esquerdos. A truncação esquerda seria útil para a análise de eventos múltiplos/recorrentes por paciente ou para a análise da coorte de casos. Foi desenvolvido um código para estudos de caso-coorte (Pintilie et al.23) e pode ser obtido dos autores. Zhou et al.24 extended the F &G model to accommodate stratified data and will also have a version for cluster data. Neste ponto, o código pode ser obtido dos autores para ambos os casos, mas é provável que seja submetido à CRAN.
STATA 11 implementou recentemente o modelo F &G. É preciso estar ciente de que os grafos obtidos usando STATA são preditivos ao invés de grafos de probabilidade observados. Existem duas advertências quando as curvas previstas são utilizadas: a) as linhas aparecem sempre como se a proporcionalidade de riscos é satisfeita, e b) o número de passos em cada curva será maior do que o número de eventos em cada subgrupo, dando a impressão de que há mais eventos do que realmente há.
conclusões
a disponibilidade de grandes conjuntos de dados com acompanhamento completo para vários objectivos está a aumentar continuamente. Há também uma necessidade crescente de análises que estão relacionadas com um objectivo preciso, como a morte por insuficiência cardíaca, o controlo de doenças ou o controlo de doenças locais. Todos estes parâmetros podem potencialmente ter CR. Por conseguinte, é essencial que o CR seja considerado desde a fase de concepção até à interpretação dos resultados. Enquanto o modelo Cox PH pode ter um valor limitado quando a independência é considerada, as estimativas do KM não são corretas e não podem ser interpretadas. Assim, é necessário aplicar técnicas específicas como os modelos CIF e F&G disponibilizados em R e parcialmente em STATA.
conflitos de interesses
nenhum declarado.