Riemann Tensor

Riemann tensor (Schutz 1985) , även känd Riemann-Christoffel krökning tensor (Weinberg 1972, s. 133; Arfken 1985, s. 123) eller Riemann krökning tensor (Misner et al. 1973, s. 218), är en tensor med fyra index som är användbar i allmän relativitet. Andra viktiga allmänna relativistiska tensorer så att Ricci krökning tensor och skalär krökning kan definieras i termer av .

Riemann tensor är på något sätt den enda tensor som kan konstrueras frånmetrisk tensor och dess första och andra derivat,

(1)

där är Christoffel-symboler av den första typen och är ett kommaderivat (Schmutzer 1968, s. 108; Weinberg 1972). I en dimension, . I fyra dimensioner finns 256 komponenter. Att använda sig av symmetri relationer,

(2)

antalet oberoende komponenter reduceras till 36. Använda villkoret

(3)

antalet koordinater minskar till 21. Slutligen, med hjälp av

(4)

20 oberoende komponenter lämnas (Misner et al. 1973, s. 220-221; Arfken 1985, s.123-124).

i allmänhet anges antalet oberoende komponenter i dimensioner av

(5)

de ”fyrdimensionella pyramidaltalen”, vars första värden är 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Antalet skalärer som kan konstrueras från och är

(6)

(Weinberg 1972). De första värdena är då 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).

i termer av Jacobi tensor ,

(7)

låt

(8)

där kvantiteten inuti är en Christoffel-symbol av den andra typen. Sedan

(9)

uppdelad i sin enklaste nedbrytning i dimensioner,

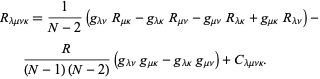(10)

här, är Ricci krökning tensor, är skalär krökning, och är Weyl tensor.