Transformación de Cabeza de familia
Transformación de Cabeza de familia (también «Reflexión de Cabeza de familia») es una transformación de reflexión ortogonal:
- refleja los vectores en las columnas de la matriz de tal manera que
- el primer vector tiene todos los ceros excepto el primer elemento
La Matriz de Transformación
Transformación de reflexión:
Propiedades
Las matrices de cabeza de familia son simétricas y ortogonales: son matrices de reflexión
Derivación
Así que tenemos $P = I – 2vv^T T:
Hacemos uso de transformaciones para la puesta a cero de los elementos
Descomposición QR
Como en el caso de la Descomposición LU, donde hemos aplicado una serie de Gauss de Transformación de los cambios, podemos hacer lo mismo y realizar una serie de Transformaciones de Householder
- así que si seleccionamos $y = \pm e_1$ (donde $e_1$ es la matriz con 1 en la posición 1 y el resto son ceros)
- a continuación, volverá a cero todos los elementos de $x$, excepto la primera
- por lo tanto por la elección adecuada de $H$ podemos tomar $A$ y cero todos los sub-diagonal los elementos
- pueden hacer eso varias veces por cada columna de $A$
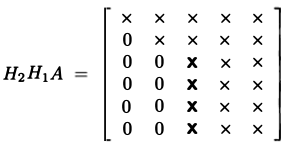
De esta manera podemos realizar la Descomposición QR:
Descomposición de Hessenberg
En lugar de usarla para reducir la matriz a Triangular, podemos usar Transformación de Cabeza de familia para reducir una matriz a Matriz de Hessenberg