![]()
nejobecnější nuceni podobě Duffing rovnice je
|
(1)
|
v Závislosti na zvolené parametry, rovnice může mít řadu speciálních forem. Například bez tlumení a bez vynucení ![]() a při znaménku plus se rovnice stane
a při znaménku plus se rovnice stane
|
(2)
|
(Bender a Orszag 1978, str. 547; Zwillinger 1997, str. 122). Tato rovnice může zobrazovat chaotické chování. Pro ![]() rovnice představuje „tvrdou pružinu“ a pro
rovnice představuje „tvrdou pružinu“ a pro ![]() představuje „měkkou pružinu“.“Pokud
představuje „měkkou pružinu“.“Pokud ![]() , křivky fázového portrétu jsou uzavřeny.
, křivky fázového portrétu jsou uzavřeny.
Pokud místo toho jsme si ![]() ,
, ![]() , resetovat hodiny tak, že
, resetovat hodiny tak, že ![]() a znaménkem minus, rovnice je pak
a znaménkem minus, rovnice je pak
|
(3)
|
Toto může být napsáno jako systém prvního řádu obyčejné diferenciální rovnice jako
|
(4)
|
|||
|
(5)
|
(Wiggins 1990, str. 5), která, v nevynucených případě, snižuje k
|
(6)
|
|||
|
(7)
|
(Wiggins 1990, str. 6; Ott 1993, str. 3).
pevné body sada provázaných diferenciálních rovnic jsou dány
|
(8)
|
takže ![]() , a
, a
|
(9)
|
|||
|
(10)
|
dává ![]() . Pevné body jsou proto
. Pevné body jsou proto ![]() ,
, ![]() , a
, a ![]() .
.
analýza stability pevných bodů může být bod linearizací rovnic. Rozlišování dává
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
což lze zapsat jako maticová rovnice
|
(14)
|
Zkoumání stability bod (0,0):
|
(15)
|
|
(16)
|
Ale ![]() , tak
, tak ![]() je reálné. Od
je reálné. Od ![]() bude vždy jeden kladný kořen, takže tento pevný bod je nestabilní. Nyní se podívejte na (
bude vždy jeden kladný kořen, takže tento pevný bod je nestabilní. Nyní se podívejte na (![]() , 0). Charakteristická rovnice je
, 0). Charakteristická rovnice je
|
(17)
|
který má kořeny
|
(18)
|
Pro ![]() ,
, ![]() , takže bod je asymptoticky stabilní. Pokud
, takže bod je asymptoticky stabilní. Pokud ![]() ,
, ![]() , takže bod je lineárně stabilní (Wiggins 1990, str. 10). Nicméně, pokud
, takže bod je lineárně stabilní (Wiggins 1990, str. 10). Nicméně, pokud ![]() , radikální dává imaginární část a reálná část je
, radikální dává imaginární část a reálná část je ![]() , takže bod je nestabilní. Pokud
, takže bod je nestabilní. Pokud ![]() ,
, ![]() , který má kladné reálné kořeny, takže bod je nestabilní. Pokud
, který má kladné reálné kořeny, takže bod je nestabilní. Pokud ![]() , pak
, pak ![]() , takže oba kořeny jsou kladné a bod je nestabilní.
, takže oba kořeny jsou kladné a bod je nestabilní.
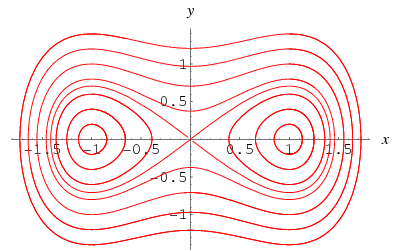
zajímavé je, že zvláštní případ ![]() bez vynucení,
bez vynucení,
|
(19)
|
|||
|
(20)
|
může být integrován do kvadratury. Rozlišování (19) a připojování (20) dává
|
(21)
|
vynásobením obou stran ![]() dává
dává
|
(22)
|
Ale to může být napsáno
|
(23)
|
takže máme invariantní pohybu ![]() ,
,
|
(24)
|
Řešení pro ![]() dává
dává
|
(25)
|
|
(26)
|
so
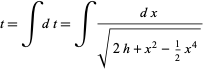 |
(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion ![]() satisfies
satisfies
|
(28)
|
|
(29)
|
takže Duffing rovnice oscilátoru jsou dány Hamiltoniansystem