![]()
den mest generelle tvunget form Av Duffing ligningen er
|
(1)
|
Avhengig av parametrene som er valgt, kan ligningen ta en rekke spesielle former. For eksempel, uten demping og ingen tvang, ![]() og tar plustegnet, blir ligningen
og tar plustegnet, blir ligningen
|
(2)
|
(Bender Og Orszag 1978, s. 547; Zwillinger 1997, s. 122). Denne ligningen kan vise kaotisk oppførsel. For ![]() representerer ligningen en «hard fjær», og for
representerer ligningen en «hard fjær», og for ![]() representerer den en «myk fjær».»Hvis
representerer den en «myk fjær».»Hvis ![]() , er faseportrettkurvene stengt.
, er faseportrettkurvene stengt.
hvis vi i stedet tar ![]() ,
, ![]() , tilbakestill klokken slik at
, tilbakestill klokken slik at ![]() , og bruk minustegnet, er ligningen da
, og bruk minustegnet, er ligningen da
|
(3)
|
dette kan skrives som et system av førsteordens ordinære differensialligninger som
|
(4)
|
|||
|
(5)
|
( Wiggins 1990, s. 5) som i det uforstyrrede tilfellet reduserer til
|
(6)
|
|||
|
(7)
|
(Wiggins 1990, s. 6; Ott 1993, s. 3).
de faste punktene i dette settet av koblede differensialligninger er gitt ved
|
(8)
|
så ![]() , og
, og
|
(9)
|
|||
|
(10)
|
gir ![]() . De faste punktene er derfor
. De faste punktene er derfor ![]() ,
, ![]() , og
, og ![]() .
.
Analyse av stabiliteten til de faste punktene kan være punkt ved å linearisere ligningene. Differensiering gir
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
som kan skrives som matriseligningen
|
(14)
|
Undersøker stabiliteten til punktet (0,0):
|
(15)
|
|
(16)
|
men ![]() , så
, så ![]() er ekte. Siden
er ekte. Siden ![]() , vil det alltid være en positiv rot, så dette faste punktet er ustabilt. Se nå på (
, vil det alltid være en positiv rot, så dette faste punktet er ustabilt. Se nå på (![]() , 0). Den karakteristiske ligningen er
, 0). Den karakteristiske ligningen er
|
(17)
|
som har røtter
|
(18)
|
for ![]() ,
, ![]() , så er punktet asymptotisk stabilt. Hvis
, så er punktet asymptotisk stabilt. Hvis ![]() ,
, ![]() , så punktet er lineært stabilt (Wiggins 1990, s. 10). Men hvis
, så punktet er lineært stabilt (Wiggins 1990, s. 10). Men hvis ![]() , radikalet gir en imaginær del og den virkelige delen er
, radikalet gir en imaginær del og den virkelige delen er ![]() , så punktet er ustabilt. Hvis
, så punktet er ustabilt. Hvis ![]() ,
, ![]() , som har en positiv reell rot, så poenget er ustabilt. Hvis
, som har en positiv reell rot, så poenget er ustabilt. Hvis ![]() , så
, så ![]() , så begge røttene er positive og punktet er ustabilt.
, så begge røttene er positive og punktet er ustabilt.
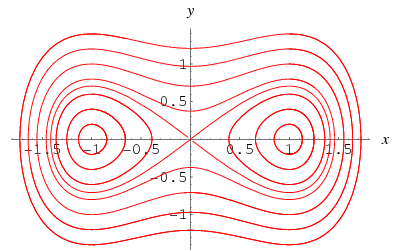
Interessant, det spesielle tilfellet ![]() uten tvang,
uten tvang,
|
(19)
|
|||
|
(20)
|
kan integreres med kvadraturer. Differensiering (19) og pluggingin (20) gir
|
(21)
|
Multiplisere begge sider med ![]() gir
gir
|
(22)
|
men dette kan skrives
|
(23)
|
så vi har en invariant av bevegelse ![]() ,
,
|
(24)
|
Løsning for ![]() gir
gir
|
(25)
|
|
(26)
|
so
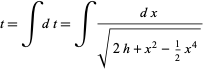 |
(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion ![]() satisfies
satisfies
|
(28)
|
|
(29)
|
så ligningene Til Duffingoscillatoren er gitt Av Hamiltoniansystemet