Duffing differentialekvation

den mest generella tvångsformen av Duffing-ekvationen är

(1)

beroende på de valda parametrarna kan ekvationen ta ett antal specialformer. Till exempel, utan dämpning och ingen tvingning, och med plustecknet blir ekvationen

(2)

(Bender och Orszag 1978, s. 547; Zwillinger 1997, s.122). Denna ekvation kan visa kaotiskt beteende. För representerar ekvationen en ”hård fjäder” och för representerar den en ”mjuk fjäder.”Om är fasporträttkurvorna stängda.

om vi istället tar , , Återställ klockan så att och använd minustecknet, ekvationen är då

(3)

detta kan skrivas som ett system av första ordningens vanliga differentialekvationer som

			(4)
			(5)

(Wiggins 1990, s. 5) som i det ofrivilliga fallet minskar till

			(6)
			(7)

(Wiggins 1990, s. 6; Ott 1993, s.3).

de fasta punkterna i denna uppsättning kopplade differentialekvationer ges av

(8)

så , och

			(9)
			(10)

ger . De fasta punkterna är därför , , och .

analys av stabiliteten hos de fasta punkterna kan vara punkt genom att linjärisera ekvationerna. Differentiering ger

			(11)
			(12)
			(13)

som kan skrivas som matrisekvationen

(14)

undersöka stabiliteten i punkten (0,0):

(15)

(16)

men , så är verklig. Eftersom kommer det alltid att finnas en positiv rot, så denna fasta punkt är instabil. Titta nu på (, 0). Den karakteristiska ekvationen är

(17)

som har rötter

(18)

för , , så är punkten asymptotiskt stabil. Om , , så punkten är linjärt stabil (Wiggins 1990, s. 10). Men om , radikalen ger en imaginär del och den verkliga delen är , så punkten är instabil. Om , , som har en positiv verklig rot, så punkten är instabil. Om , då , så båda rötterna är positiva och punkten är instabil.

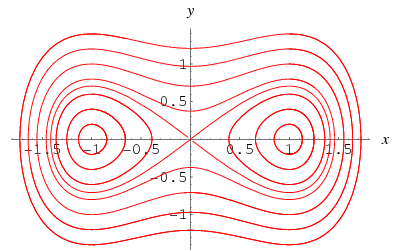
intressant, det speciella fallet utan att tvinga,

			(19)
			(20)

kan integreras med kvadraturer. Differentierande (19) och pluggingin (20) ger

(21)

multiplicera båda sidor med ger

(22)

men detta kan skrivas

(23)

så vi har en invariant av rörelse ,

(24)

lösa för ger

(25)

(26)

so

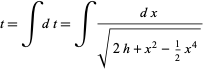(27)

(Wiggins 1990, p. 29).

Note that the invariant of motion satisfies

(28)

(29)

så ekvationerna för Duffing-oscillatorn ges av Hamiltoniansystemet