Articles

Duffing differentiaaliyhtälö

author
2 Min Read

lataa Mathematica Notebook

Duffing-yhtälön yleisin pakotettu muoto on

x^..+deltax^.+(betax^3+ / - omega_0^2x)=gammacos(omegat+phi).
(1)

valittujen parametrien mukaan yhtälö voi saada useita erityisiä muotoja. Esimerkiksi ilman vaimennusta ja ilman pakottamista, delta=gamma = 0 ja ottaen plus-merkin, yhtälöstä tulee

x^..+ omega_0^2x + betax^3=0
(2)

(bender and Orszag 1978, s. 547; Zwillinger 1997, s. 122). Tämä yhtälö voi näyttää kaoottista käyttäytymistä. beta0 yhtälö edustaa ”kovaa jousta”, ja beta0 se edustaa ”pehmeää jousta.”Jos beta0, vaihemuotokäyrät ovat suljettuja.

jos sen sijaan otetaan beta = 1, omega_0 = 1, nollataan kello niin, että phi = 0, ja käytetään miinusmerkkiä, yhtälö on sitten

x^..+deltax^.+(x^3-x)=gammacos(omegat).
(3)

tämä voidaan kirjoittaa ensimmäisen kertaluvun tavallisten differentiaaliyhtälöiden järjestelmänä

x^. = y,
(4)
j^. = x-x^3-deltay+gammacos (omegat)
(5)

(Wiggins 1990, s. 5), joka unforced-tapauksessa pelkistää

x^. = y
(6)
j^. = x-x^3-deltay
(7)

(Wiggins 1990, s. 6; Ott 1993, s. 3).

tämän kytkettyjen differentiaaliyhtälöiden joukon kiinteät pisteet saadaan

x^.=y=0,
(8)

joten y=0, ja

j^. = x-x^3-deltay
(9)
= x (1-x^2)-0
(10)

antaa x=0,+/-1. Kiinteät pisteet ovat siis (-1,0), (0,0), ja (1,0).

kiintopisteiden stabiilisuuden analyysi voidaan pisteyttää linearisoimalla yhtälöt. Erottelu antaa

x^.. = j^.
(11)
= x-x^3-deltay
(12)
j^.. = (1-3x^2) x^.- deltay^.,
(13)

joka voidaan kirjoittaa matriisiyhtälönä

=.
(14)

pisteen vakauden tutkiminen (0,0):

|0-lambda 1; 1-delta-lambda / =lambda (lambda+delta)-1 = lambda^2+lambdadelta-1=0
(15)
lambda_+/-^((0,0))=1/2(-delta+/-sqrt (Delta^2+4)).
(16)

mutta delta^2=0, joten lambda_+/-^((0,0)) se on totta. Koska sqrt (delta^2+4)|delta|, on aina yksi positiivinen juuri, joten tämä kiintopiste on epävakaa. Katso nyt (+/-1, 0). Karakteristinen yhtälö on

|0-lambda 1; -2-delta-lambda / =lambda (lambda+delta)+2 = lambda^2+lambdadelta+2=0,
(17)

jolla on juuret

lambda_+/-^((+/-1,0))=1/2(-delta+/-sqrt(Delta^2-8)).
(18)

delta0, R0, joten piste on asymptoottisesti stabiili. Jos delta=0, lambda_+/-^((+/-1,0))=+/-isqrt (2), joten piste on lineaarisesti stabiili (Wiggins 1990, s. 10). Kuitenkin, jos delta in (- 2sqrt(2),0), radikaali antaa imaginaariosan ja reaaliosa on 0, joten piste on epästabiili. Jos delta= - 2sqrt(2), lambda_+/-^((+/-1,0))=sqrt (2), jolla on positiivinen reaalijuuri, joten piste on epävakaa. Jos delta-2sqrt(2), niin |delta|sqrt (Delta^2-8), joten molemmat juuret ovat positiivisia ja piste on epävakaa.

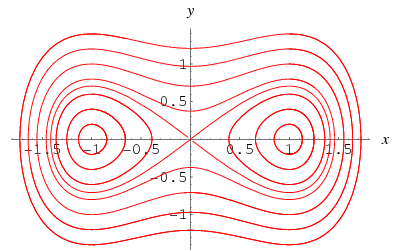
DuffingOscillatorPhasePortrait

kiinnostavaa, erikoistapaus delta=0 ilman pakottamista,

x^. = y
(19)
j^. = x-x^3,
(20)

voidaan integroida kvadratureilla. Differentiating (19) ja pluggingin (20) antaa

x^..=j^.=x-x^3.
(21)

kertomalla molemmat puolet x^. antaa

x^..x^.- x^.x + x^.x^3=0.
(22)

mutta tämä voidaan kirjoittaa

d/(dt) (1 / 2x^.^2-1 / 2x^2+1 / 4x^4)=0,
(23)

joten meillä on invariant liikkeen h,

h=1 / 2x^.^2-1 / 2x^2+1 / 4x^4.
(24)

ratkaiseminen x^.^2 antaa

x^.^2=((dx)/(dt))^2=2h+x^2-1/2x^4
(25)
(dx)/(dt)=sqrt(2h+x^2-1/2x^4),
(26)

so

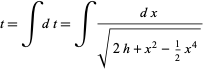t=intdt=int(dx)/(sqrt(2h+x^2-1/2x^4))
(27)

(Wiggins 1990, p. 29).

Note that the invariant of motion h satisfies

x^.=(partialh)/(partialx^.) =(partialh)/(partialy)
(28)
(partialh)/(partialx)=-x+x^3=-y^.,
(29)

Duffing oskillaattorin yhtälöt saadaan siis Hamiltoniansystem

You might also like

Vastaa

Sähköpostiosoitettasi ei julkaista.