hvis du har læst det forrige indlæg om, hvad der er en induktor, lad os gå videre til det næste niveau, hvad er induktansformel kredsløb.
nu hvor induktoren er føjet til vores liste over passive elementer, er det nødvendigt at udvide det kraftfulde værktøj til Serie-parallel kombination. Vi skal vide, hvordan man finder den tilsvarende induktans af et serieforbundet eller parallelforbundet sæt induktorer, der findes i praktiske kredsløb.
Serieinduktorer
overvej en serieforbindelse af N-induktorer, som vist i figur.(1a), med det tilsvarende kredsløb vist i figur.(1b).

induktorerne har den samme strøm gennem dem. Anvendelse KVL til sløjfen,

udskiftning af vk= Lk di / dt resulterer i
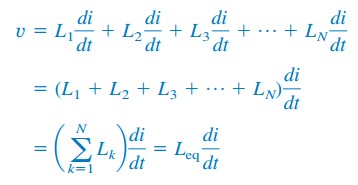
hvor

således,
den ækvivalente induktans af serieforbundne induktorer er summen af de individuelle induktanser.
induktorer i serie kombineres på nøjagtig samme måde som modstande i serie.
parallelle induktorer
vi overvejer nu en parallel forbindelse af N induktorer, som vist i figur.(2a), med tilsvarende kredsløb i figur.(2b). Induktorerne har samme spænding på tværs af dem. Brug af KCL,

men


derfor

hvor
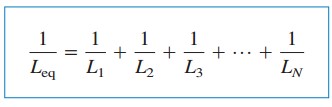
den indledende strøm i (t0) gennem Lekv ved t= t0 forventes af KCL at være summen af induktorstrømmene ved t0. Således ifølge ligning.(5),
![]()
ifølge ligning.(6),
den ækvivalente induktans af parallelle induktorer er den gensidige af summen af de gensidige induktanser af de enkelte induktanser.
Bemærk, at induktorerne parallelt kombineres på samme måde som modstande parallelt.
for to induktorer parallelt (N = 2), ligning.(6) bliver
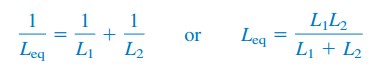
induktans formel kredsløb eksempler
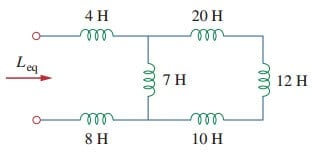
1. Find den tilsvarende induktans af kredsløbet vist i figur.(3).
løsning:
10-H, 12-H og 20-H induktorer er i serie; således kombinerer dem en 42-H induktans. Denne 42-H induktor er parallelt med 7-H induktoren, så de kombineres for at give


denne 6-H induktor er i serie med 4-H og 8-H induktorer. Derfor,
![]()
2. For kredsløbet i figur.(4),
i(t) = 4(2 − e−10t) mA. Hvis i2(0) = -1 mA, find:
(a) i1(0);
(b) v(t), v1(t) og v2(t);
(c) i1(t) og i2 (t).

løsning:
(A) fra i (t) = 4 (2−e-10t) mA, i(0) = 4(2 − 1) = 4 mor.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(c) den nuværende i1 opnås som


tilsvarende,


Bemærk, at i1(t) + i2(t) = i(t).