Einfache Ornstein-Uhlenbeck-Modelle

Schätzung evolutionärer Optima

Dieses Tutorial zeigt, wie man ein Ornstein-Uhlenbeck-Modell spezifiziert, bei dem der optimale Phänotyp unter Zweigen einer zeitkalibrierten Phylogenie (fehlende Referenz) unter Verwendung der Datensätze von (log) Körpergröße über Wirbeltierklassen von (fehlende Referenz). Wir bieten die probabilistische grafische Modelldarstellung jeder Komponente für dieses Tutorial. Nachdem Sie das Modell angegeben haben, schätzen Sie die Parameter der Ornstein-Uhlenbeck-Evolution mithilfe von Markov Chain Monte Carlo (MCMC).

Ornstein-Uhlenbeck-Modell

Unter dem einfachen Ornstein-Uhlenbeck (OU) -Modell wird angenommen, dass sich ein kontinuierliches Zeichen zu einem optimalen Wert, $ \ theta $, entwickelt. Das Zeichen entwickelt sich stochastisch nach einem Driftparameter, $ \ sigma ^ 2 $. Das Zeichen wird durch die Anpassungsrate $ \ alpha $ zum Optimum gezogen; größere Alpha-Werte zeigen an, dass das Zeichen stärker in Richtung $ \ theta $ gezogen wird. Wenn sich das Zeichen von $ \ theta $ entfernt, bestimmt der Parameter $ \ alpha $, wie stark das Zeichen zurückgezogen wird. Aus diesem Grund wird $ \ alpha $ manchmal als „Gummiband“ -Parameter bezeichnet. Wenn der Anpassungsparameter $ \ alpha = 0 $ ist, wird das OU-Modell auf das BM-Modell reduziert. Das resultierende grafische Modell ist recht einfach, da die Wahrscheinlichkeit der fortlaufenden Zeichen nur von der Phylogenie (die wir in diesem Tutorial als bekannt annehmen) und den drei OU-Parametern () abhängt.

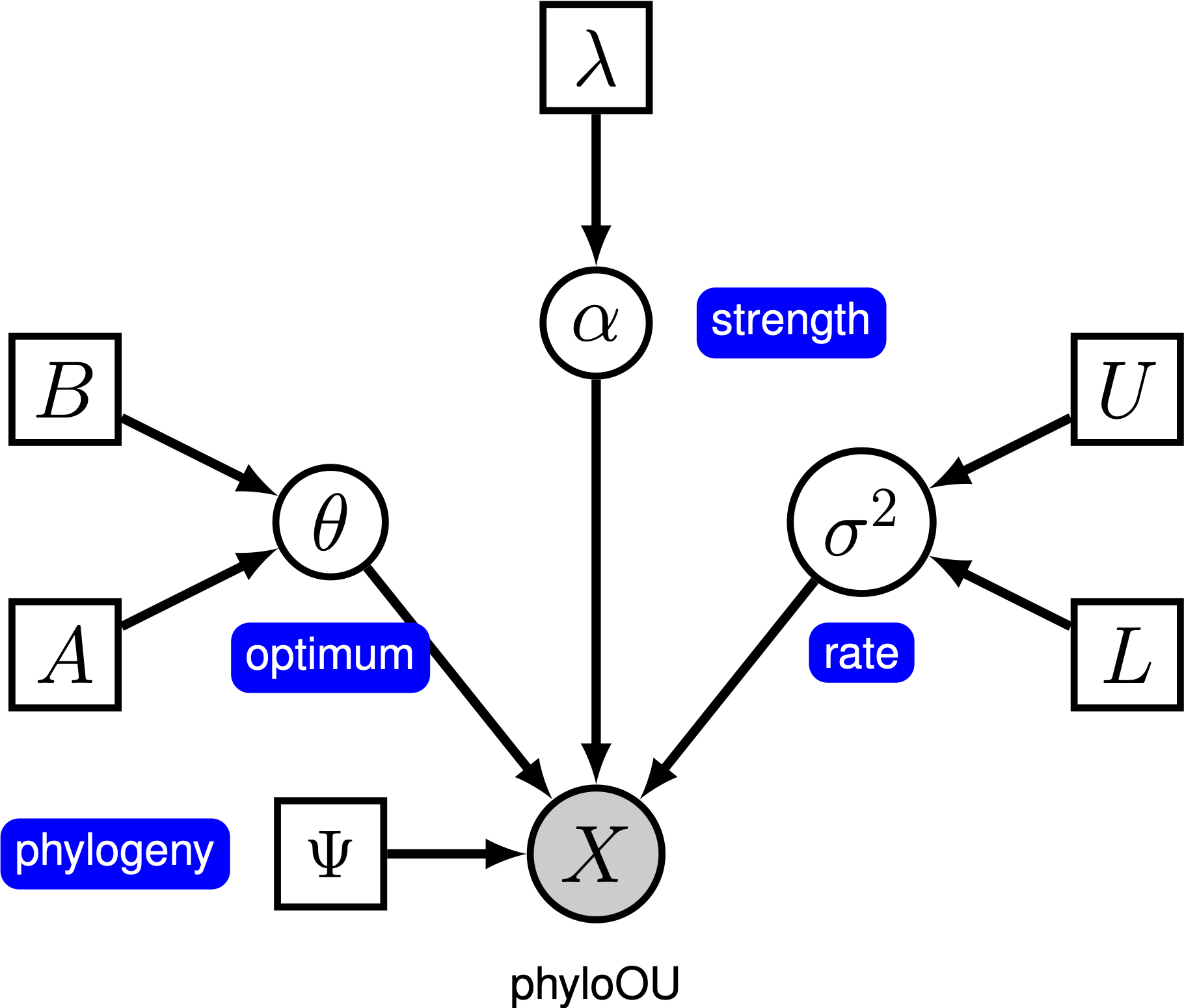
In diesem Tutorial verwenden wir die 66 Wirbeltierphylogenien und (Log-) Körpergrößendatensätze von (Landis and Schraiber 2017).

⇨ Die vollständige Spezifikation des OU-Modells befindet sich in der Datei mcmc_OU.Rev.

Lesen Sie die Daten

Wir entscheiden zunächst, welche der 66 Wirbeltierdatensätze verwendet werden sollen. Hier gehen wir davon aus, dass wir den ersten Datensatz (Acanthuridae) analysieren, aber Sie sollten sich frei fühlen, einen der Datensätze auszuwählen.

dataset <- 1

Jetzt lesen wir den (zeitkalibrierten) Baum ein, der unserem ausgewählten Datensatz entspricht.

T <- readTrees("data/trees.nex")

Als nächstes lesen wir die Zeichendaten für denselben Datensatz ein.

data <- readContinuousCharacterData("data/traits.nex")

Zusätzlich initialisieren wir eine Variable für unseren Vektor ofmoves und Monitore:

moves = VectorMoves()monitors = VectorMonitors()

Angeben des Modells

Baummodell

In diesem Tutorial gehen wir davon aus, dass der Baum ohne Fläche bekannt ist. Wir erstellen einen konstanten Knoten für den Baum, der der beobachteten Phylogenie entspricht.

tree <- T

Ratenparameter

Die stochastische Evolutionsrate wird durch den Ratenparameter $ \ sigma ^ 2 $ gesteuert. Wir zeichnen den Ratenparameter aus einem loguniformen Prior. Dieser Prior ist auf der Log-Skala einheitlich, was bedeutet, dass er Unkenntnis über die Größenordnung der Rate darstellt.

sigma2 ~ dnLoguniform(1e-3, 1)

Um die posteriore Verteilung von $ \ sigma ^ 2 $ zu schätzen, müssen wir einen MCMC-Vorschlagsmechanismus bereitstellen, der auf diesem Knoten arbeitet. Da $\sigma^2$ ein Ratenparameter ist und daher positiv sein muss, verwenden wir eine Skalierungsbewegung namens mvScale .

moves.append( mvScale(sigma2, weight=1.0) )

Anpassungsparameter

Die Geschwindigkeit der Anpassung an das Optimum wird durch den Parameter $\alpha $ bestimmt. Wir ziehen $ \ alpha $ aus einer exponentiellen Vorverteilung und platzieren einen Skalenvorschlag darauf.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

Wir ziehen den optimalen Wert aus einem vagen einheitlichen Prior von -10 bis 10 (Sie sollten diesen Prior ändern, wenn Ihr Charakter außerhalb dieses Bereichs liegt). Da dieser Parameter positiv oder negativ sein kann, verwenden wir eine Folienbewegung, um Änderungen während der MCMC vorzuschlagen.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck-Modell

Nachdem wir nun die Parameter des Modells festgelegt haben, können wir die Zeichendaten aus dem entsprechenden phylogenetischen OU-Modell ziehen. In diesem Beispiel verwenden wir den REML-Algorithmus, um die Wahrscheinlichkeit effizient zu berechnen (Felsenstein 1985). Wir nehmen an, dass das Zeichen mit dem optimalen Wert an der Wurzel des Baumes beginnt.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

In Anbetracht dessen, dass $X $ die beobachteten Daten () , klemmen wir den data an diesen stochastischen Knoten.

X.clamp(data)

Schließlich erstellen wir ein Workspace-Objekt für das gesamte Modell mit model() . Beachten Sie, dass Workspace-Objekte mit dem Operator = initialisiert werden und selbst nicht Teil des Bayes’schen grafischen Modells sind. Die Funktion model() durchläuft das gesamte Modelldiagramm und findet alle Knoten in dem von uns angegebenen Modell. Dieses Objekt bietet eine bequeme Möglichkeit, auf das gesamte Modellobjekt und nicht nur auf einen einzelnen DAG-Knoten zu verweisen.

mymodel = model(theta)

Ausführen einer MCMC-Analyse

Angeben von Monitoren

Für unsere MCMC-Analyse müssen wir einen Vektor von Monitoren einrichten, um die Zustände unserer Markov-Kette aufzuzeichnen. Die Monitorfunktionen heißen alle mn*, wobei * der Platzhalter ist, der den Monitortyp darstellt. Zuerst initialisieren wir den Modellmonitor mit der Funktion mnModel. Dadurch wird eine neue Monitorvariable erstellt, die die Zustände für alle Modellparameter ausgibt, wenn sie an eine MCMC-Funktion übergeben wird.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

Erstellen Sie außerdem einen Bildschirmmonitor, der die Zustände der angegebenen Variablen mit mnScreen an den Bildschirm meldet:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

Initialisieren und Ausführen der MCMC-Simulation

Mit einem vollständig spezifizierten Modell, einer Reihe von Monitoren und einer Reihe von Bewegungen können wir nun den MCMC-Algorithmus einrichten, der Parameterwerte im Verhältnis zu ihrer posterioren Wahrscheinlichkeit abtastet. Die Funktion mcmc() erstellt unser MCMC-Objekt:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

Führen Sie nun das MCMC aus:

mymcmc.run(generations=50000)

Wenn die Analyse abgeschlossen ist, befinden sich die überwachten Dateien in Ihremausgabeverzeichnis.

⇨ Die Rev-Datei zur Durchführung dieser Analyse: mcmc_OU.Rev

Zeichen, die sich unter dem OU-Prozess entwickeln, tendieren zu einer stationären Verteilung, die eine Normalverteilung mit Mittelwert $ \ theta $ und Varianz $ \ sigma ^ 2 \ div 2 \ alpha $ ist. Wenn also die Evolutionsraten hoch sind (oder die Zweige im Baum relativ lang sind), kann es schwierig sein, $ \ sigma ^ 2 $ und $ \ alpha $ getrennt zu schätzen, da beide die langfristige Varianz des Prozesses bestimmen. Wir können sehen, ob dies unsere Analyse beeinflusst, indem wir die gemeinsame posteriore Verteilung der Parameter in Tracer untersuchen. Wenn die Parameter positiv korreliert sind, sollten wir zögern, ihre Randverteilungen zu interpretieren (dh keine Rückschlüsse auf die Anpassungsrate oder den Varianzparameter separat zu ziehen).

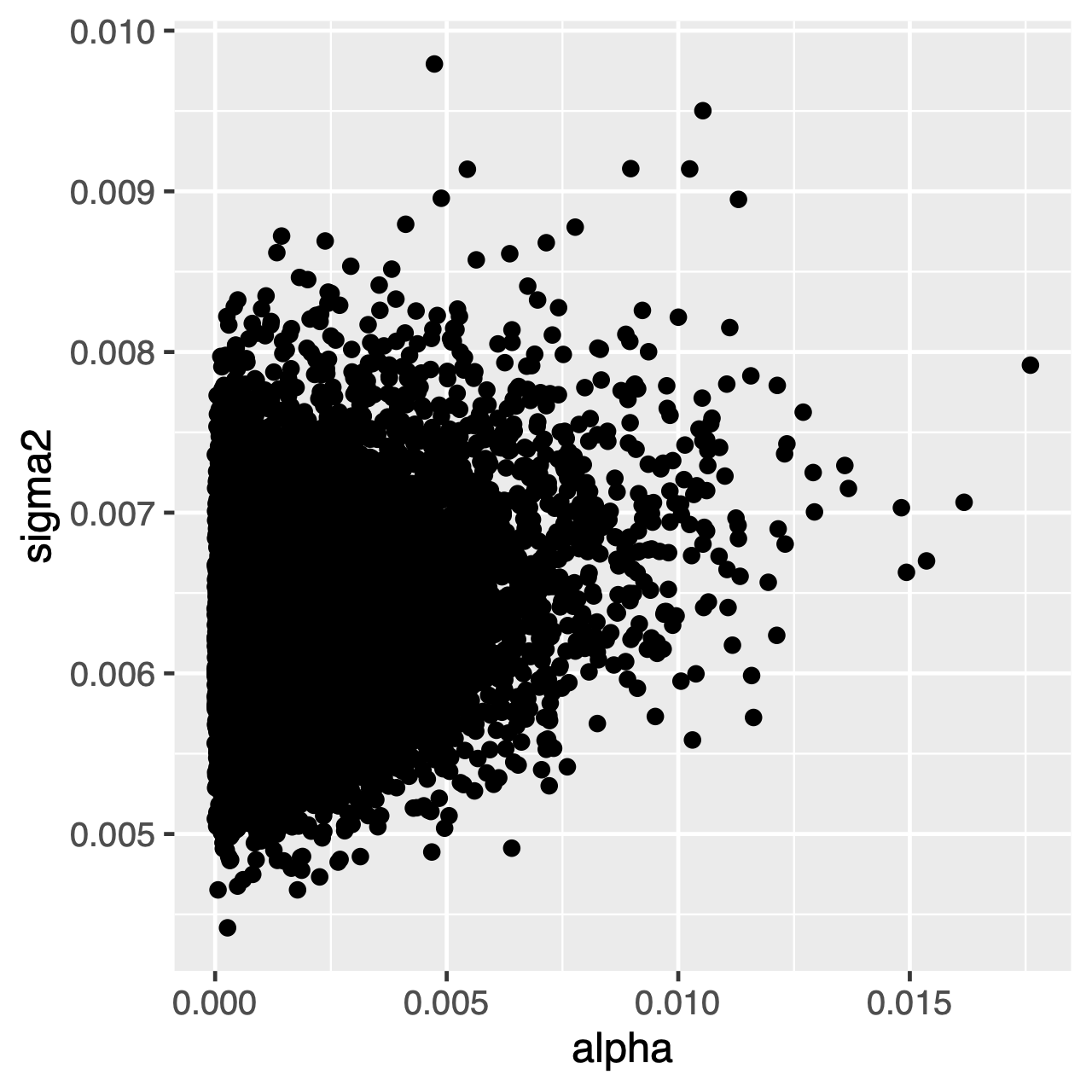
Übung 1

• Führen Sie eine MCMC-Simulation durch, um die posteriore Verteilung des OU-Optimums (theta) abzuschätzen.
• Laden Sie die generierte Ausgabedatei in Tracer: Was ist die mittlere posteriore Schätzung von theta und was ist die geschätzte HPD?
• Verwenden Sie Tracer, um die posterioren Gelenkverteilungen von alpha und sigma2 zu vergleichen. Sind diese Parameter korreliert oder nicht korreliert?
• Vergleichen Sie den vorherigen Mittelwert mit dem posterioren Mittelwert. (Hinweis: Verwenden Sie das optionale Argument underPrior=TRUE in der Funktion mymcmc.run() ) Unterscheiden sie sich (zB)? Liegt der posteriore Mittelwert außerhalb des vorherigen 95% -Wahrscheinlichkeitsintervalls?

Vergleich von OU- und BM-Modellen

Da wir nun sowohl BM- als auch OU-Modelle anpassen können, möchten wir natürlich wissen, welches Modell besser passt. In diesem Abschnitt erfahren Sie, wie Sie mit Reversible-Jump Markov Chain Monte Carlo die Passform von OU- und BM-Modellen vergleichen.

Modellauswahl mit Reversible-Jump MCMC

Um die Hypothese zu testen, dass sich ein Charakter zu einem selektiven Optimum entwickelt, stellen wir uns zwei Modelle vor. Das erste Modell, bei dem es keine Anpassung an das Optimum gibt, ist der Fall, wenn $\alpha = 0 $ . Das zweite Modell entspricht dem OU-Modell mit $\alpha > 0$. Dies funktioniert, weil die Brownsche Bewegung ein Sonderfall des OU-Modells ist, wenn die Anpassungsrate 0 ist. Da $ \ alpha $ ein stetiger Parameter ist, wird eine Standard-Markov-Kette leider niemals Zustände besuchen, in denen jeder Wert genau gleich 0 ist. Glücklicherweise können wir den reversiblen Sprung verwenden, damit die Markov-Kette den Besuch des Brownschen Bewegungsmodells in Betracht ziehen kann. Dies beinhaltet die Angabe der vorherigen Wahrscheinlichkeit für jedes der beiden Modelle und die Bereitstellung der vorherigen Verteilung für $ \ alpha $ für das OU-Modell.

Mit rjMCMC kann die Markov-Kette die beiden Modelle proportional zu ihrer posterioren Wahrscheinlichkeit besuchen. Die posteriore Wahrscheinlichkeit des Modells $ i $ ist einfach der Bruchteil der Stichproben, bei denen die Kette dieses Modell besuchte. Da wir auch einen Prior für die Modelle angeben, können wir einen Bayes-Faktor für das OU-Modell berechnen als:

\

wobei $P( \text{OU-Modell} \mid X) $ und $ P( \text{OU-Modell}) $ sind die posteriore Wahrscheinlichkeit bzw. die vorherige Wahrscheinlichkeit des OU-Modells.

Reversible-Jump zwischen OU- und BM-Modellen

Um rjMCMC zu aktivieren, müssen wir einfach einen reversible-jump vor dem relevanten Parameter $ \alpha $ platzieren. Wir können den Prior auf alpha so ändern, dass er entweder einen konstanten Wert von 0 annimmt oder aus einer Prior-Verteilung stammt. Schließlich spezifizieren wir eine vorherige Wahrscheinlichkeit auf dem OU-Modell von p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

Wir stellen dann einen Reversible-Jump-Vorschlag auf alpha bereit, der Änderungen zwischen den beiden Modellen vorschlägt.

moves.append( mvRJSwitch(alpha, weight=1.0) )

Zusätzlich bieten wir den normalen mvScale -Vorschlag an, wenn das MCMC das OU-Modell besucht.

moves.append( mvScale(alpha, weight=1.0) )

Wir schließen eine Variable ein, die den Wert 1 hat, wenn die Kette das OU-Modell besucht, und eine entsprechende Variable, die den Wert 1 hat, wenn sie das BM-Modell besucht. Auf diese Weise können wir die posteriore Wahrscheinlichkeit der Modelle leicht berechnen, da wir lediglich den posterioren Mittelwert dieses Parameters berechnen müssen.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

Der Anteil der Stichproben, für den is_OU = 1 die posteriore Wahrscheinlichkeit des OU-Modells ist. Alternativ entspricht die posteriore mittlere Schätzung dieser Indikatorvariablen der posterioren Wahrscheinlichkeit des OU-Modells. Diese Werte können in der obigen Bayes-Faktorgleichung verwendet werden, um die Bayes-Faktorunterstützung für beide Modelle zu berechnen.

1. Felsenstein J. 1985. Phylogenien und die Vergleichsmethode. Der amerikanische Naturforscher.:1-15.10.1086/284325
2. Höhna S., Heath T.A., Boussau B., Landis M.J., Ronquist F., Hülsenbeck J.P. 2014. Probabilistische grafische Modelldarstellung in der Phylogenetik. Systematische Biologie. 63:753-771.10.1093/sysbio/syu039
3. Landis MJ, Schraiber JG 2017. Gepulste Evolution geformte moderne Wirbelkörpergrößen. Proceedings der Nationalen Akademie der Wissenschaften. 114:13224-13229.10.1073/pnas.1710920114