Wenn Sie den vorherigen Beitrag darüber gelesen haben, was eine Induktivität ist, gehen wir zur nächsten Ebene über, was ist die Induktivitätsformelschaltungen.
Nun, da die Induktivität zu unserer Liste der passiven Elemente hinzugefügt wurde, ist es notwendig, das leistungsstarke Werkzeug der Serien-Parallel-Kombination zu erweitern. Wir müssen wissen, wie man die äquivalente Induktivität eines in Reihe oder parallel geschalteten Satzes von Induktivitäten in praktischen Schaltungen findet.
Serieninduktivitäten
Betrachten Sie eine Reihenschaltung von N Induktivitäten, wie in Abbildung gezeigt.(1a), mit der Ersatzschaltung in Abbildung gezeigt.(1b).

Die Induktivitäten haben den gleichen Strom durch sie. Anwenden von KVL auf die Schleife,

Das Ersetzen von vk = Lk di / dt führt zu
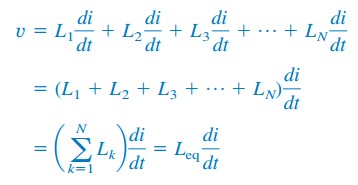
wo

So,
Die äquivalente Induktivität von in Reihe geschalteten Induktivitäten ist die Summe der einzelnen Induktivitäten.
Induktivitäten in Reihe werden genauso kombiniert wie Widerstände in Reihe.
Parallele Induktivitäten
Wir betrachten nun eine Parallelschaltung von N Induktivitäten, wie in Abbildung gezeigt.(2a), mit der Ersatzschaltung in Abbildung.(2b). Die Induktivitäten haben die gleiche Spannung. Mit KCL,

Aber


daher

wo
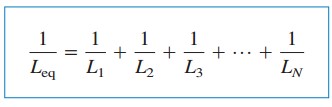
Der Anfangsstrom i(t0) durch Leq bei t= t0 wird von KCL als Summe der Induktorströme bei t0 erwartet. Also nach Gleichung.(5),
![]()
Nach Gleichung.(6),
Die äquivalente Induktivität paralleler Induktivitäten ist der Kehrwert der Summe der Kehrwerte der einzelnen Induktivitäten.
Beachten sie, dass die induktivitäten parallel sind kombiniert in der gleichen weise wie widerstände in parallel.
Für zwei Induktivitäten parallel (N = 2), Gleichung.(6) wird
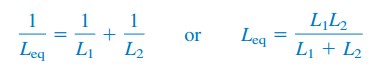
Induktivität Formel Schaltungen Beispiele
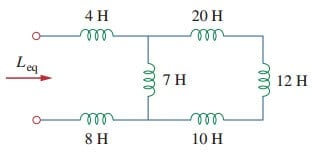
1. Finden Sie die äquivalente Induktivität der Schaltung in Abbildung gezeigt.(3).
Lösung:
Die 10-H-, 12-H- und 20-H-Induktivitäten sind in Reihe geschaltet; Daher ergibt ihre Kombination eine 42-H-Induktivität. Diese 42-H-Induktivität ist parallel zur 7-H-Induktivität, so dass sie kombiniert werden, um


Diese 6-H induktivität ist in serie mit die 4-H und 8-H induktivitäten. Daher,
![]()
2. Für die Schaltung in Fig.(4),
ich(t) = 4(2 − e-10t) mA. Wenn i2(0) = -1 mA ist, finden Sie:
(a) i1(0);
(b) v(t), v1 (t) und v2 (t);
(c) i1 (t) und i2 (t).

Lösung:
(a) Von i(t) = 4 (2 − e−10t) mA, i(0) = 4(2 − 1) = 4 mA.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
( c) Der Strom i1 ergibt sich als


Ähnlich,


Beachten Sie, dass i1(t) + i2(t) = i(t).