Équation Différentielle Duffing

La forme forcée la plus générale de l’équation de Duffing est

(1)

Selon les paramètres choisis, l’équation peut prendre un certain nombre de formes spéciales. Par exemple, sans amortissement et sans forçage, et en prenant le signe plus, l’équation devient

(2)

( Bender et Orszag 1978, p. 547; Zwillinger 1997, p. 122). Cette équation peut afficher un comportement chaotique. Pour , l’équation représente un « ressort dur » et pour , elle représente un « ressort mou. » Si , les courbes de portrait de phase sont fermées.

Si à la place nous prenons , , réinitialisez l’horloge de sorte que , et utilisez le signe moins, l’équation est alors

(3)

Cela peut être écrit comme un système d’équations différentielles ordinaires du premier ordre comme

			(4)
			(5)

( Wiggins 1990, p. 5) qui, dans le cas non forcé, se réduit à

			(6)
			(7)

( Wiggins 1990, p. 6; Ott 1993, p. 3).

Les points fixes de cet ensemble d’équations différentielles couplées sont donnés par

(8)

donc , et

			(9)
			(10)

donner . Les points fixes sont donc , , et .

L’analyse de la stabilité des points fixes peut être ponctuelle en linéarisant les équations. Différencier donne

			(11)
			(12)
			(13)

qui peut s’écrire comme l’équation matricielle

(14)

Examen de la stabilité du point (0,0):

(15)

(16)

Mais , donc est réel. Puisque , il y aura toujours une racine positive, donc ce point fixe est instable. Regardez maintenant (, 0). L’équation caractéristique est

(17)

qui a des racines

(18)

Pour , , le point est donc asymptotiquement stable. Si , , donc le point est linéairement stable (Wiggins 1990, p. 10). Cependant, si , le radical donne une partie imaginaire et la partie réelle est , donc le point est instable. Si , , qui a une racine réelle positive, donc le point est instable. Si , alors , donc les deux racines sont positives et le point est instable.

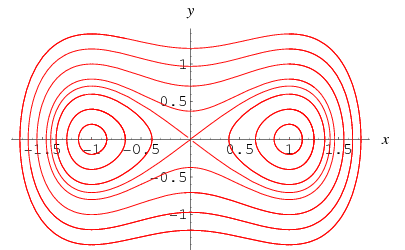
Fait intéressant, le cas particulier sans forçage,

			(19)
			(20)

peut être intégré par quadratures. Différencier (19) et enficher (20) donne

(21)

Multipliant les deux côtés par donne

(22)

Mais cela peut être écrit

(23)

nous avons donc un invariant de mouvement ,

(24)

Résolution pour donne

(25)

(26)

so

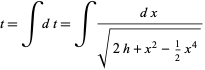(27)

(Wiggins 1990, p. 29).

Note that the invariant of motion satisfies

(28)

(29)

ainsi, les équations de l’oscillateur de Duffing sont données par le système hamiltonien