![]()
a Duffing egyenlet legáltalánosabb kényszerített formája
|
(1)
|
a választott paraméterektől függően az egyenlet számos speciális formát ölthet. Például csillapítás és kényszerítés nélkül ![]() és a pluszjelet figyelembe véve az egyenlet a következő lesz
és a pluszjelet figyelembe véve az egyenlet a következő lesz
|
(2)
|
(Bender és Orsag 1978, 547. o.; Zwillinger 1997, 122. o.). Ez az egyenlet kaotikus viselkedést mutathat. ![]() esetén az egyenlet “kemény rugót”,
esetén az egyenlet “kemény rugót”, ![]() esetén pedig “puha rugót” jelent.”Ha
esetén pedig “puha rugót” jelent.”Ha ![]() , a fázis portré görbék zárva vannak.
, a fázis portré görbék zárva vannak.
ha ehelyett vesszük ![]() ,
, ![]() , állítsa vissza az órát úgy, hogy
, állítsa vissza az órát úgy, hogy ![]() , és használja a mínuszjelet, akkor az egyenlet
, és használja a mínuszjelet, akkor az egyenlet
|
(3)
|
ez lehet írni, mint egy rendszer elsőrendű rendes differenciálegyenletek, mint
|
(4)
|
|||
|
(5)
|
(Wiggins 1990, 5. o.), amely kényszerítetlen esetben a következőkre redukálódik
|
(6)
|
|||
|
(7)
|
(Wiggins 1990, 6. o.; Ott 1993, 3. o.).
a kapcsolt differenciálegyenletek ezen halmazának rögzített pontjait a
|
(8)
|
tehát ![]() , és
, és
|
(9)
|
|||
|
(10)
|
ad ![]() . A rögzített pontok tehát
. A rögzített pontok tehát ![]() ,
, ![]() , és
, és ![]() .
.
a rögzített pontok stabilitásának elemzése pont lehet az egyenletek linearizálásával. Differenciáló ad
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
amely lehet írni, mint a mátrix egyenlet
|
(14)
|
a pont stabilitásának vizsgálata (0,0):
|
(15)
|
|
(16)
|
de ![]() , tehát
, tehát ![]() valódi. Mivel
valódi. Mivel ![]() , mindig lesz egy pozitív gyökér, tehát ez a fix pont instabil. Most nézd meg (
, mindig lesz egy pozitív gyökér, tehát ez a fix pont instabil. Most nézd meg (![]() , 0). A jellemző egyenlet
, 0). A jellemző egyenlet
|
(17)
|
amelynek gyökerei vannak
|
(18)
|
mert ![]() ,
, ![]() , tehát a pont aszimptotikusan stabil. Ha
, tehát a pont aszimptotikusan stabil. Ha ![]() ,
, ![]() , tehát a pont lineárisan stabil (Wiggins 1990, 10. o.). Ha azonban
, tehát a pont lineárisan stabil (Wiggins 1990, 10. o.). Ha azonban ![]() , a gyök egy képzeletbeli részt ad, a valós rész pedig
, a gyök egy képzeletbeli részt ad, a valós rész pedig ![]() , tehát a pont instabil. Ha
, tehát a pont instabil. Ha ![]() ,
, ![]() , amelynek pozitív valós gyökere van, tehát a pont instabil. Ha
, amelynek pozitív valós gyökere van, tehát a pont instabil. Ha ![]() , akkor
, akkor ![]() , tehát mindkét gyökér pozitív és a pont instabil.
, tehát mindkét gyökér pozitív és a pont instabil.
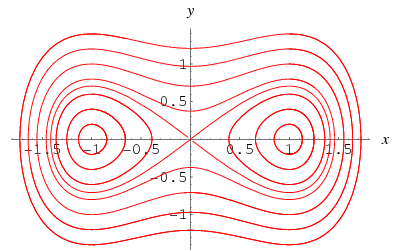
érdekes, hogy a különleges eset ![]() nem kényszerítve,
nem kényszerítve,
|
(19)
|
|||
|
(20)
|
kvadratúrákkal integrálható. Differenciáló (19) és duggingin (20) ad
|
(21)
|
szorozzuk meg mindkét oldalt ![]() ad
ad
|
(22)
|
de ezt meg lehet írni
|
(23)
|
tehát van egy invariáns a mozgás ![]() ,
,
|
(24)
|
megoldása ![]() ad
ad
|
(25)
|
|
(26)
|
so
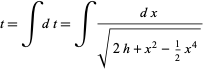 |
(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion ![]() satisfies
satisfies
|
(28)
|
|
(29)
|
tehát a Duffing oszcillátor egyenleteit a Hamilton adjarendszer