Semplice Ornstein-Uhlenbeck Modelli

La stima Evolutivo Optima

Questo tutorial viene illustrato come specificare un Ornstein-Uhlenbeck in cui il modello ottimale fenotipo è ipotizzato costante tra i rami di un tempo, calibrata per la filogenesi (mancante di riferimento) utilizzando il set di dati di (log) corpo-dimensioni in tutta vertebrati cladi da (mancante di riferimento). Forniamo la rappresentazione del modello grafico probabilistico di ogni componente per questo tutorial. Dopo aver specificato il modello, si stimano i parametri dell’evoluzione di Ornstein-Uhlenbeck utilizzando la catena Markov Monte Carlo (MCMC).

Modello di Ornstein-Uhlenbeck

Sotto il semplice modello di Ornstein-Uhlenbeck (OU), si presume che un carattere continuo si evolva verso un valore ottimale, $\theta$. Il personaggio si evolve stocasticamente secondo un parametro di deriva, sigma \ sigma ^ 2$. Il personaggio è tirato verso l’optimum dal tasso di adattamento, alpha \ alpha alpha; valori più grandi di alfa indicano che il carattere è tirato più forte verso \ \ theta$. Quando il personaggio si allontana da \ \ theta$, il parametro alpha\alpha determines determina la forza con cui il personaggio viene tirato indietro. Per questo motivo, sometimes \ alpha is è talvolta indicato come un parametro “elastico”. Quando il parametro rate of adaptation parameter \ alpha = 0 0, il modello OU collassa nel modello BM. Il modello grafico risultante è abbastanza semplice, poiché la probabilità dei caratteri continui dipende solo dalla filogenesi (che assumiamo essere conosciuta in questo tutorial) e dal parametro three OU ().

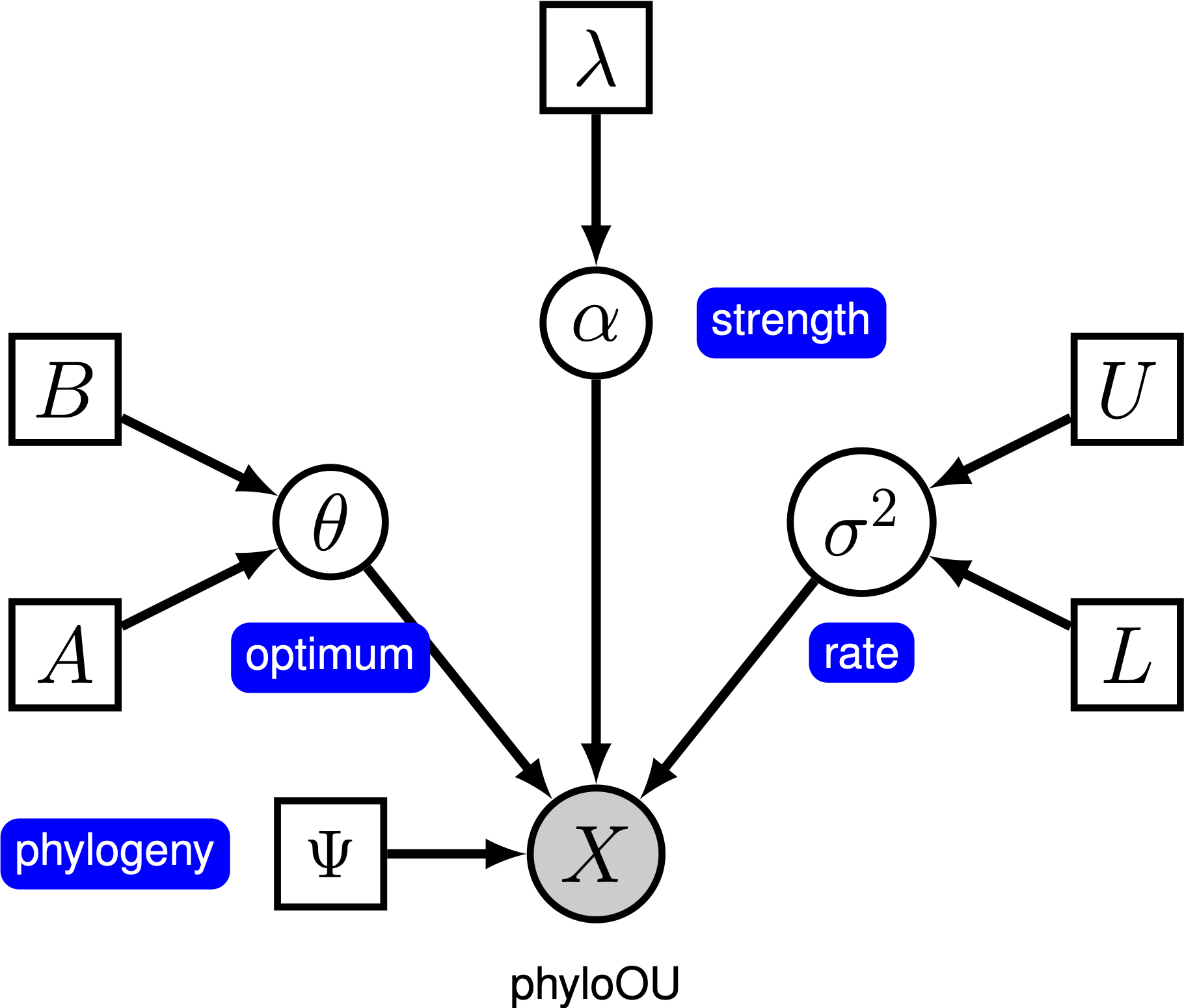
In questo tutorial, usiamo le 66 filogenie vertebrati e (log) set di dati di dimensioni corporee da (Landis e Schraiber 2017).

The la specifica completa del modello OU è nel file chiamato mcmc_OU.Rev.

Leggi i dati

Iniziamo decidendo quale dei 66 set di dati vertebrati utilizzare. Qui, assumiamo che stiamo analizzando il primo set di dati (Acanthuridae), ma dovresti sentirti libero di scegliere uno qualsiasi dei set di dati.

dataset <- 1

Ora, leggiamo nell’albero (calibrato nel tempo) corrispondente al nostro set di dati scelto.

T <- readTrees("data/trees.nex")

Successivamente, leggiamo i dati dei caratteri per lo stesso set di dati.

data <- readContinuousCharacterData("data/traits.nex")

Inoltre, inizializziamo una variabile per il nostro vettore ofmoves e monitor:

moves = VectorMoves()monitors = VectorMonitors()

Specificando il modello

Modello ad albero

In questo tutorial, assumiamo che l’albero sia noto senza area. Creiamo un nodo costante per l’albero che corrisponde alla filogenesi osservata.

tree <- T

Parametro Rate

Il tasso stocastico di evoluzione è controllato dal parametro rate, sigma \ sigma ^ 2$. Disegniamo il parametro rate da un loguniform prior. Questo precedente è uniforme sulla scala del registro, il che significa che rappresenta l’ignoranza sull’ordine di grandezza del tasso.

sigma2 ~ dnLoguniform(1e-3, 1)

Per stimare la distribuzione posteriore di sigma \ sigma ^ 2 must, dobbiamo fornire un meccanismo di proposta MCMC che opera su questo nodo. Poiché $ \ sigma^2 is è un parametro di tasso, e deve quindi essere positivo, usiamo una mossa di ridimensionamento chiamata mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

Parametro di adattamento

Il tasso di adattamento verso l’optimum è determinato dal parametro alpha \ alpha$. Disegniamo $ \ alpha from da una distribuzione precedente esponenziale e posizioniamo una proposta di scala su di essa.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

Tracciamo il valore ottimale da una vaga uniforme prima che va da -10 a 10 (dovresti cambiarlo prima se il tuo personaggio è al di fuori di questo intervallo). Poiché questo parametro può essere positivo o negativo, usiamo una mossa diapositiva per proporre modifiche durante MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck model

Ora che abbiamo specificato i parametri del modello, possiamo trarre i dati dei caratteri dal corrispondente modello filogenetico OU. In questo esempio, usiamo l’algoritmo REML per calcolare in modo efficiente la probabilità (Felsenstein 1985). Assumiamo che il carattere inizi al valore ottimale alla radice dell’albero.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

Notando che X X is è il dato osservato (), blocchiamo data a questo nodo stocastico.

X.clamp(data)

Infine, creiamo un oggetto workspace per l’intero modello con model(). Ricorda che gli oggetti workspace sono inizializzati con l’operatore = e non sono essi stessi parte del modello grafico bayesiano. La funzione model() attraversa l’intero grafico del modello e trova tutti i nodi nel modello specificato. Questo oggetto fornisce un modo conveniente per fare riferimento all’intero oggetto modello, piuttosto che a un singolo nodo DAG.

mymodel = model(theta)

Esecuzione di un’analisi MCMC

Specificando i monitor

Per la nostra analisi MCMC, dobbiamo impostare un vettore di monitor per registrare gli stati della nostra catena di Markov. Le funzioni del monitor sono tutte chiamate mn*, dove * è il carattere jolly che rappresenta il tipo di monitor. Innanzitutto, inizializzeremo il monitor del modello utilizzando la funzione mnModel. Questo crea una nuova variabile monitor che emetterà gli stati per tutti i parametri del modello quando passati in una funzione MCMC.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

Inoltre, creare un monitor dello schermo che riporterà gli stati delle variabili specificate sullo schermo con mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

Inizializzando ed eseguendo la simulazione MCMC

Con un modello completamente specificato, un set di monitor e un set di mosse, possiamo ora impostare l’algoritmo MCMC che campionerà i valori dei parametri inproporzione alla loro probabilità posteriore. La funzione mcmc() creerà il nostro oggetto MCMC:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

Ora, eseguire il MCMC:

mymcmc.run(generations=50000)

Quando l’analisi è completa, avrai i file monitorati nella tua directory output.

The il file Rev per eseguire questa analisi: mcmc_OU.Rev

I caratteri che si evolvono sotto il processo OU tenderanno verso una distribuzione stazionaria, che è una distribuzione normale con media mean\theta and e varianza vari\sigma^2 \div 2\alpha$. Pertanto, se i tassi di evoluzione sono alti (o i rami nell’albero sono relativamente lunghi), può essere difficile stimare separately\sigma^2 separately e separately\alpha separately separatamente, poiché entrambi determinano la varianza a lungo termine del processo. Possiamo vedere se questo influenza la nostra analisi esaminando la distribuzione posteriore articolare dei parametri in Tracer. Quando i parametri sono correlati positivamente, dovremmo esitare a interpretare le loro distribuzioni marginali (cioè, non fare inferenze sul tasso di adattamento o sul parametro di varianza separatamente).

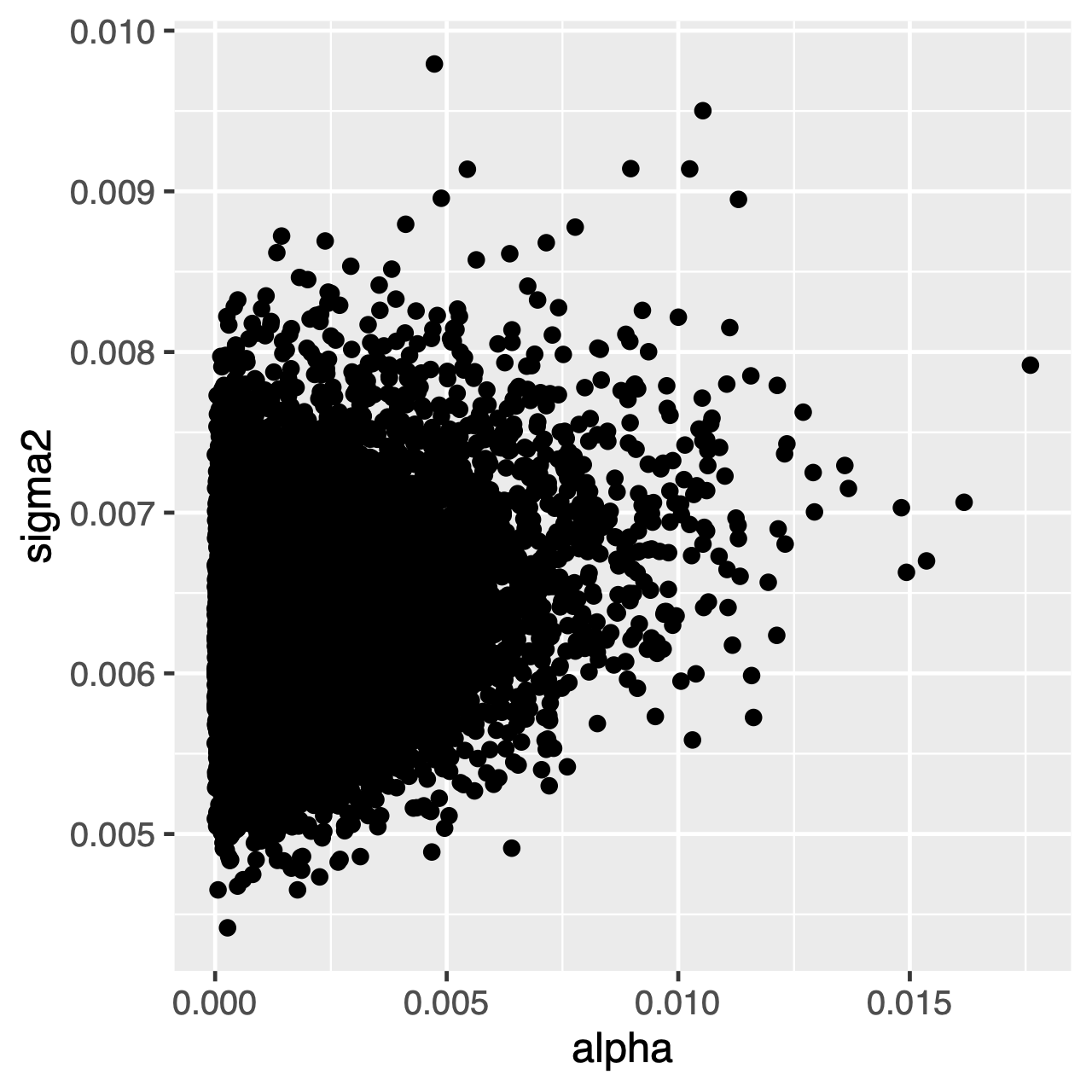
Esercizio 1

• Eseguire una simulazione MCMC per stimare la distribuzione posteriore dell’OU optimum (theta).
• Carica il file di output generato in Tracer: Qual è la stima posteriore media di theta e qual è l’HPD stimato?
• Utilizzare Tracer per confrontare le distribuzioni posteriori articolari di alphae sigma2. Questi parametri sono correlati o non correlati?
• Confronta la media precedente con la media posteriore. (Suggerimento: usa l’argomento opzionale underPrior=TRUE nella funzione mymcmc.run()) Sono diversi (ad esempio,)? La media posteriore è al di fuori del precedente intervallo di probabilità del 95%?

Confronto OU e BM modelli

Ora che siamo in grado di adattarsi sia BM e OU modelli, potremmo naturalmente voler sapere quale modello fa si adatta meglio. In questa sezione, impareremo come utilizzare reversible-jump Markov chain Monte Carlo per confrontare la vestibilità dei modelli OU e BM.

Selezione del modello utilizzando Reversible-Jump MCMC

Per testare l’ipotesi che un personaggio evolva verso un optimum selettivo, immaginiamo due modelli. Il primo modello, dove non c’è adattamento verso l’ottimale, è il caso quando alpha\alpha = 0$. Il secondo modello corrisponde al modello OU con alpha \ alpha > 0$. Questo funziona perché il moto browniano è un caso speciale del modello OU quando il tasso di adattamento è 0. Sfortunatamente, poiché $ \ alpha parameters è un parametro continuo, una catena di Markov standard non visiterà mai stati in cui ogni valore è esattamente uguale a 0. Fortunatamente, possiamo usare il salto reversibile per consentire alla catena di Markov di considerare di visitare il modello di moto browniano. Ciò implica specificare la probabilità precedente su ciascuno dei due modelli e fornire la distribuzione precedente per $\alpha.per il modello OU.

L’utilizzo di rjMCMC consente alla catena di Markov di visitare i due modelli in proporzione alla loro probabilità posteriore. La probabilità posteriore del modello i i is è semplicemente la frazione di campioni in cui la catena stava visitando quel modello. Poiché specifichiamo anche un precedente sui modelli, possiamo calcolare un fattore di Bayes per il modello OU come:

\

dove respectively P( \text{OU model} \mid X) respectively e P P( \text{OU model}) respectively sono rispettivamente la probabilità posteriore e la probabilità precedente del modello OU.

Reversible-jump tra i modelli OU e BM

Per abilitare rjMCMC, dobbiamo semplicemente posizionare un reversible-jump prima sul parametro pertinente, alpha\alpha$. Possiamo modificare il precedente su alpha in modo che prenda un valore costante di 0 o sia tratto da una distribuzione precedente. Infine, specifichiamo una probabilità precedente sul modello OU di p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

Forniamo quindi una proposta di salto reversibile su alpha che propone modifiche tra i due modelli.

moves.append( mvRJSwitch(alpha, weight=1.0) )

Inoltre, forniamo la normale proposta mvScale per quando il MCMC sta visitando il modello OU.

moves.append( mvScale(alpha, weight=1.0) )

Includiamo una variabile che ha un valore 1 quando la catena sta visitando il modello OU e una variabile corrispondente che ha valore 1 quando sta visitando il modello BM. Questo ci permetterà di calcolare facilmente la probabilità posteriore dei modelli perché abbiamo semplicemente bisogno di calcolare il valore medio posteriore di questo parametro.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

La frazione di campioni per i quali is_OU = 1 è la probabilità posteriore del modello OU. In alternativa, la stima media posteriore di questa variabile indicatore corrisponde alla probabilità posteriore del modello OU. Questi valori possono essere utilizzati nell’equazione del fattore di Bayes sopra per calcolare il supporto del fattore di Bayes per entrambi i modelli.

1. Felsenstein J. 1985. Filogenesi e metodo comparativo. Il naturalista americano.:1-15.10.1086/284325
2. Höhna S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. 2014. Rappresentazione di modelli grafici probabilistici in filogenetica. Biologia sistematica. 63:753-771. 10. 1093/sysbio / syu039
3. Landis M. J., Schraiber J. G. 2017. L’evoluzione pulsata ha modellato le dimensioni moderne del corpo dei vertebrati. Atti dell’Accademia Nazionale delle Scienze. 114: 13224-13229. 10. 1073 / pnas.1710920114