ケインズ消費関数は二つの主要な仮説に基づいていた。 第一に、消費する限界傾向は0と1の間にあります。 第二に、平均的な消費傾向は、所得が上昇するにつれて低下する。 初期の実証的研究はこれらの仮説と一致していた。 しかし、第二次世界大戦後、収入が増加するにつれて貯蓄は上昇しなかったことが観察された。 したがって、ケインジアンモデルは消費現象を説明することができず、したがって、時間間選択の理論が開発された。 時間間選択の分析は、1834年にJohn Raeによって「資本の社会学的理論」で導入されました。 その後、1889年のEugen von Böhm-Bawerkと1930年のIrving Fisherはモデルを詳しく説明しました。 一時的な選択に基づく他のいくつかのモデルには、Franco Modiglianiによって提案されたライフサイクル仮説とMilton Friedmanによって提案された恒久的所得仮説が含まれ ワラシアン均衡の概念はまた、時間間の選択を組み込むために拡張することができる。 このような均衡のウォラシアン分析では、先物価格と現物価格という二つの”新しい”価格概念が導入されています。
フィッシャーの時代間消費モデル編集委員会

アーヴィング・フィッシャーは著書『Theory of interest』(1930年)の中で時間割選択の理論を発展させた。 消費を現在の収入に関連させたケインズとは対照的に、フィッシャーのモデルは、合理的な前向きな消費者が、生涯の満足度を最大化するために、現在と未来のために消費をどのように選択するかを示した。
Fisherによると、個人の焦りは、収入の流れの4つの特徴、すなわち大きさ、時間の形、構成、リスクに依存する。 これに加えて、先見性、自己制御、習慣、人生の期待、および遺贈動機(または他人の生活への関心)は、人の焦りを決定する5つの個人的な要因であり、それが彼の時間の好みを決定します。
異なる期間にわたって消費者が行使する選択を理解するために、私たちはある期間の消費を複合商品として取ります。 消費者N{\displaystyle N{\displaystyle N{\displaystyle N}}が1つあるとする。}

商品、および二つの期間。 選好はU(x1,x2){\displaystyle U(x_{1},x_{2})}によって与えられる。{2})}

ここで、x t=(x t1,… ,x T N){\displaystyle x_{t}=(x_{t1},\dots,x_{tN})}

。 期間t{\displaystyle t{\displaystyle t}における収入}

t{\displaystyle Y_{t}}

以下である。 第1期の貯蓄はS1{\displaystyle S_{\displaystyle S_}}である。{1}}

, 期間t{\displaystyle t{\displaystyle t}での支出}

はC t{\displaystyle C_{t}}

であり、r{\displaystyle r}

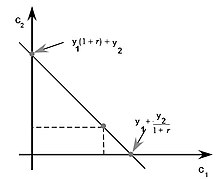
金利です。 その人が最初の期間に将来の収入に対して借りることができない場合、彼は各期間に別々の予算制約の対象となります:C1+S1≤Y1,{\displaystyle C_{1}+S_{1}\leq Y_{1},}

(1) C2≤Y2+S1(1+r). {\displaystyle C_{2}\leq Y_{2}+S_{1}(1+r). C C_{2}\leq Y_{2}+S_{1}(1+r).となります。 (2)
一方、そのような借入が可能であれば、その人は単一の時間間予算制約の対象となります:
C1+C2 1+r=Y1+Y2 1+r。 {\displaystyle C_{1}+{\frac{C_{2}}{1+r}}=Y_{1}+{\frac{Y_{2}}{1+r}}。 C_{1}+{\frac{C_{2}}{1+r}}=Y_{1}+{\frac{Y_{2}}{1+r}}です。 (3)
左側は支出の現在価値を示し、右側は収入の現在価値を示しています。 方程式に(1+r){\displaystyle(1+r)}を掛ける)}

は、対応する将来の値を提供します。
今、消費者はC1{\displaystyle C_{1}}を選択する必要があります{1}}

とC2{\displaystyle C_{2}}

U(C1,C2){\displaystyle U(C_{1},C_{2})を最大化するようにする{2})}

c1+C2/(1+r)=Y1+Y2/(1+r)となる。 {\displaystyle C_{1}+C_{2}/(1+r)=Y_{1}+Y_{2}/(1+r)である。



消費者は純救済者または純借り手であるかもしれない。 彼が純借り手でも純救済者でもない消費のレベルに最初にあれば、収入の増加は彼に彼の好みによって純救済者か純借り手をするかもしれない。 現在の収入または将来の収入の増加は、現在および将来の消費(消費平滑動機)を増加させる。
ここで、金利が上昇するシナリオを考えてみましょう。 消費者がネットセーバーである場合、彼は代替効果のために現在の期間に多くを保存し、収入効果のために現在の期間に多くを消費します。 したがって、正味の効果はあいまいになります。 しかし、消費者が純借り手である場合、彼は代替効果と収入効果のために現在の期間に消費する傾向があり、それによって彼の全体的な消費電流を減
モディリアーニのライフサイクル収入仮説編集
ライフサイクル仮説は、以下のモデルに基づいています:
max U t=∑t U(c t)(1+δ)−t{\displaystyle\max U_{t}=\sum_{t}U(C_{t})(1+\delta)-{-t}}
(1+r)−t=∑t Y t(1+r)−t+W0{\displaystyle\sum_{t}C_{t}(1+r)-{-t}=\sum_{t}Y_{t}(1+r)^{-t}+w_{0},}

ここで、
U(Ct)は期間tにおける消費から受け取った満足度、Ctは時間tにおける消費レベル、Ytは時間tにおける収入、δは時間の割合である。 嗜好(現在と将来の活動の間の個々の好みの尺度)、W0は資産を生産する所得の初期レベルです。

典型的には、人のMPC(限界消費性向)は、若い成人期には比較的高く、中年期には減少し、その人が近くにいるか退職しているときに増加する。 ライフサイクル仮説(LCH)モデルは、個々の行動を、現在の所得水準とは多少独立した生涯にわたって消費パターンを滑らかにする試みとして定義している。 このモデルは、個人が新しい家を買うこと、家族を始めること、そしてキャリアを始めることに関連する主要な購入をするかもしれないので、人生の 人生のこの段階では、個人は、これらの支出のニーズをサポートするために、将来から借りることになります。 しかし中年では、これらの支出パターンは水平になり始め、増加によって支えられるか、または多分超過しますincome.At この段階では、個々の任意の過去の借入金を返済し、彼女または彼の退職のために保存を開始します。退職すると、消費支出は減少し始めるかもしれませんが、収入は通常劇的に減少します。 生命のこの段階では、個人は死まで過去の節約を離れてdis救うか、または住んでいる。
フリードマンの永久所得仮説編集
第二次世界大戦後、消費電流が現在の収入の関数に過ぎないモデルは明らかに単純すぎることに気づいた。 長期的な平均消費傾向は、限界消費傾向がはるかに低いにもかかわらず、ほぼ一定であるように見えるという事実を説明することはできませんでした。 したがって、Milton Friedmanの永久所得仮説は、この明らかな矛盾を説明しようとするモデルの1つです。
永久所得仮説によれば、永久消費CPは永久所得YPに比例する。 永久的な収入は、おそらく平均将来所得の主観的な概念です。 永久的な消費は消費の同じような概念である。
実際の消費Cと実際の収入Yは、それぞれこれらの恒久的な構成要素に予期しない一時的な構成要素CTとYTで構成されています。
CPt=xt2ypt Ct=CPt+CTt Yt=YPt+YTt