Eenvoudige Ornstein-Uhlenbeck Modellen

Het schatten van de Evolutionaire Optima

in Deze zelfstudie ziet u hoe u een Ornstein-Uhlenbeck model waarbij de optimale fenotype wordt verondersteld constant onder de takken van een time-gekalibreerd fylogenie (ontbrekende verwijzing) met behulp van de datasets van (log) lichaam-grootte over gewervelde subtypes van (ontbrekende verwijzing). We bieden de probabilistische grafische modelweergave van elk onderdeel voor deze tutorial. Na het specificeren van het model, zult u de parameters van Ornstein-Uhlenbeck evolution schatten met behulp van Markov chain Monte Carlo (MCMC).

Ornstein-Uhlenbeck Model

Onder het eenvoudige Ornstein-Uhlenbeck (OU) model wordt aangenomen dat een continu karakter evolueert naar een optimale waarde, $\theta$. Het karakter evolueert stochastisch volgens een drift parameter, $ \ sigma^2$. Het personage wordt naar het optimum getrokken door de snelheid van aanpassing, $ \ alpha$; grotere waarden van alpha geven aan dat het teken sterker naar $\theta$getrokken wordt. Als het teken weg beweegt van $\theta$, bepaalt de parameter $ \ alpha$ hoe sterk het teken terug getrokken wordt. Om deze reden wordt $\alpha$ soms aangeduid als een “elastiekje” parameter. Wanneer de snelheid van de aanpassingsparameter $ \ alpha = 0$, stort het OU-model in op het BM-model. Het resulterende grafische model is vrij eenvoudig, omdat de waarschijnlijkheid van de continue karakters alleen afhangt van de fylogenie (waarvan we aannemen dat ze bekend zijn in deze tutorial) en de drie ou parameter ().

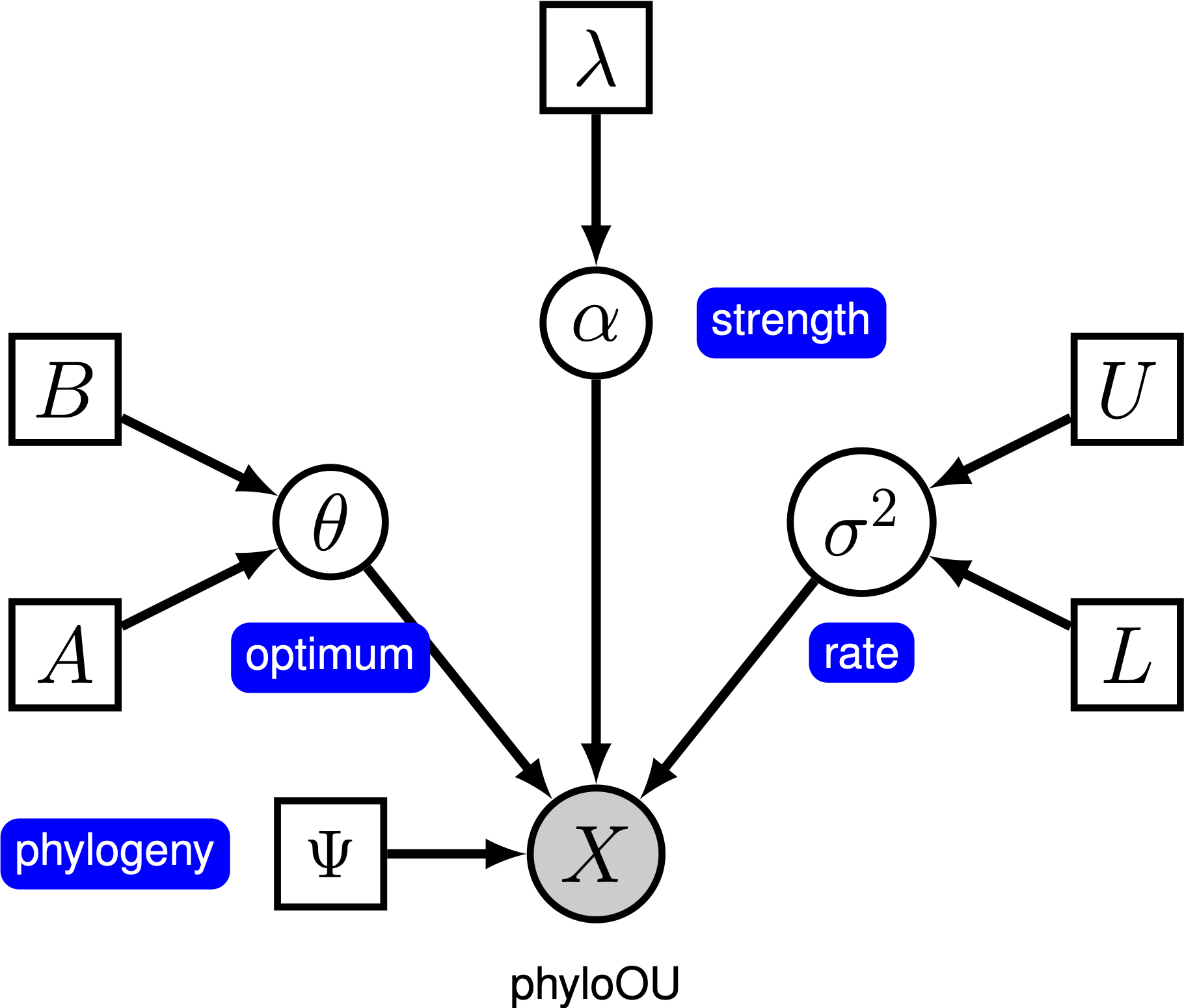
in deze tutorial gebruiken we de 66 fylogenieën van gewervelde dieren en (log) datasets van lichaamsgrootte (Landis and Schraiber 2017).

⇨ de volledige specificatie van het OU-model staat in het bestand mcmc_OU.Rev.

lees de data

we beginnen met te beslissen welke van de 66 gewervelde datasets te gebruiken. Hier gaan we ervan uit dat we de eerste dataset (Acanthuridae) analyseren, maar je moet je vrij voelen om een van de datasets te kiezen.

dataset <- 1

nu lezen we in de (tijd-gekalibreerde) boom die overeenkomt met onze gekozen dataset.

T <- readTrees("data/trees.nex")

vervolgens lezen we in de karaktergegevens voor dezelfde dataset.

data <- readContinuousCharacterData("data/traits.nex")

daarnaast initialiseren we een variabele voor onze vector van moves en monitors:

moves = VectorMoves()monitors = VectorMonitors()

het specificeren van het model

Tree model

in deze tutorial gaan we ervan uit dat de tree bekend is zonder gebied. We creëren een constante knoop voor de boom die overeenkomt met de waargenomen fylogenie.

tree <- T

snelheid parameter

de stochastische snelheid van evolutie wordt gecontroleerd door de snelheid parameter, $\sigma^2$. We trekken de rate parameter uit een loguniform prior. Deze prior is uniform op de log schaal, wat betekent dat het vertegenwoordigt onwetendheid over de Orde van grootte van het tarief.

sigma2 ~ dnLoguniform(1e-3, 1)

om de posterieure verdeling van $ \ sigma^2$ te schatten, moeten we een MCMC voorstel mechanisme bieden dat op dit knooppunt werkt. Omdat $ \ sigma^2$ Een rate parameter is, en daarom positief moet zijn, gebruiken we een schaling beweging genaamd mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

Aanpassingsparameter

de snelheid van aanpassing naar het optimum wordt bepaald door de parameter $\alpha$. We trekken $\alpha$ uit een exponentiële eerdere distributie, en plaatsen er een schaalvoorstel op.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

we trekken de optimale waarde uit een vage uniforme prior variërend van -10 tot 10 (U moet deze prior wijzigen als uw karakter buiten dit bereik valt). Omdat deze parameter positief of negatief kan zijn, gebruiken we een slide move om veranderingen voor te stellen tijdens MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck model

nu we de parameters van het model hebben gespecificeerd, kunnen we de karaktergegevens uit het overeenkomstige fylogenetische OU-model trekken. In dit voorbeeld gebruiken we het reml algoritme om de waarschijnlijkheid efficiënt te berekenen (Felsenstein 1985). We gaan ervan uit dat het karakter begint bij de optimale waarde aan de wortel van de boom.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

opmerkend dat $X$ de geobserveerde data () is, klemmen we de data op deze stochastische knoop.

X.clamp(data)

tot slot maken we een werkruimteobject voor het gehele model met model(). Onthoud dat werkruimteobjecten geïnitialiseerd zijn met de = operator, en zelf geen deel uitmaken van het Bayesiaanse grafische model. De functie model() doorkruist de gehele modelgrafiek en vindt alle knooppunten in het model dat we hebben opgegeven. Dit object biedt een handige manier om te verwijzen naar het hele model object, in plaats van slechts een enkele dag node.

mymodel = model(theta)

het uitvoeren van een MCMC-analyse

waarbij Monitors

worden gespecificeerd voor onze MCMC-analyse moeten we een vector van monitors opzetten om de toestanden van onze Markov-keten vast te leggen. De monitorfuncties worden allemaal mn* genoemd, waarbij * het jokerteken is dat het monitortype vertegenwoordigt. Eerst zullen we de modelmonitor initialiseren met behulp van de mnModel functie. Hiermee wordt een nieuwe monitorvariabele gecreëerd die de status van alle modelparameters uitvoert wanneer deze wordt doorgegeven aan een MCMC-functie.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

maak bovendien een schermmonitor aan die de statussen van gespecificeerde variabelen aan het scherm rapporteert met mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

initialiseren en uitvoeren van de MCMC simulatie

met een volledig gespecificeerd model, een set monitors en een set bewegingen, kunnen we nu het MCMC algoritme instellen dat parameterwaarden zal sampleen in verhouding tot hun posterieure waarschijnlijkheid. De functie mcmc() maakt ons MCMC-object aan:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

doe de MCMC.:

mymcmc.run(generations=50000)

wanneer de analyse is voltooid, zult u de bewaakte bestanden in youroutput directory.

⇨ het Rev bestand voor het uitvoeren van deze analyse: mcmc_OU.Rev

tekens die onder het OU-proces evolueren, neigen naar een stationaire distributie, wat een normale distributie is met gemiddelde $\theta$ en variantie $ \ sigma^2 \ div 2 \ alpha$. Daarom, als de evolutietarieven hoog zijn (of de takken in de boom relatief lang zijn), kan het moeilijk zijn om $\sigma^2$ en $\alpha$ afzonderlijk te schatten, omdat beide de lange termijn variantie van het proces bepalen. We kunnen zien of dit onze Analyse beïnvloedt door de gezamenlijke posterieure verdeling van de parameters in Tracerte onderzoeken. Wanneer de parameters positief gecorreleerd zijn, zouden we moeten aarzelen om hun marginale verdelingen te interpreteren (d.w.z., maak geen gevolgtrekkingen over de snelheid van aanpassing of de variantieparameter afzonderlijk).

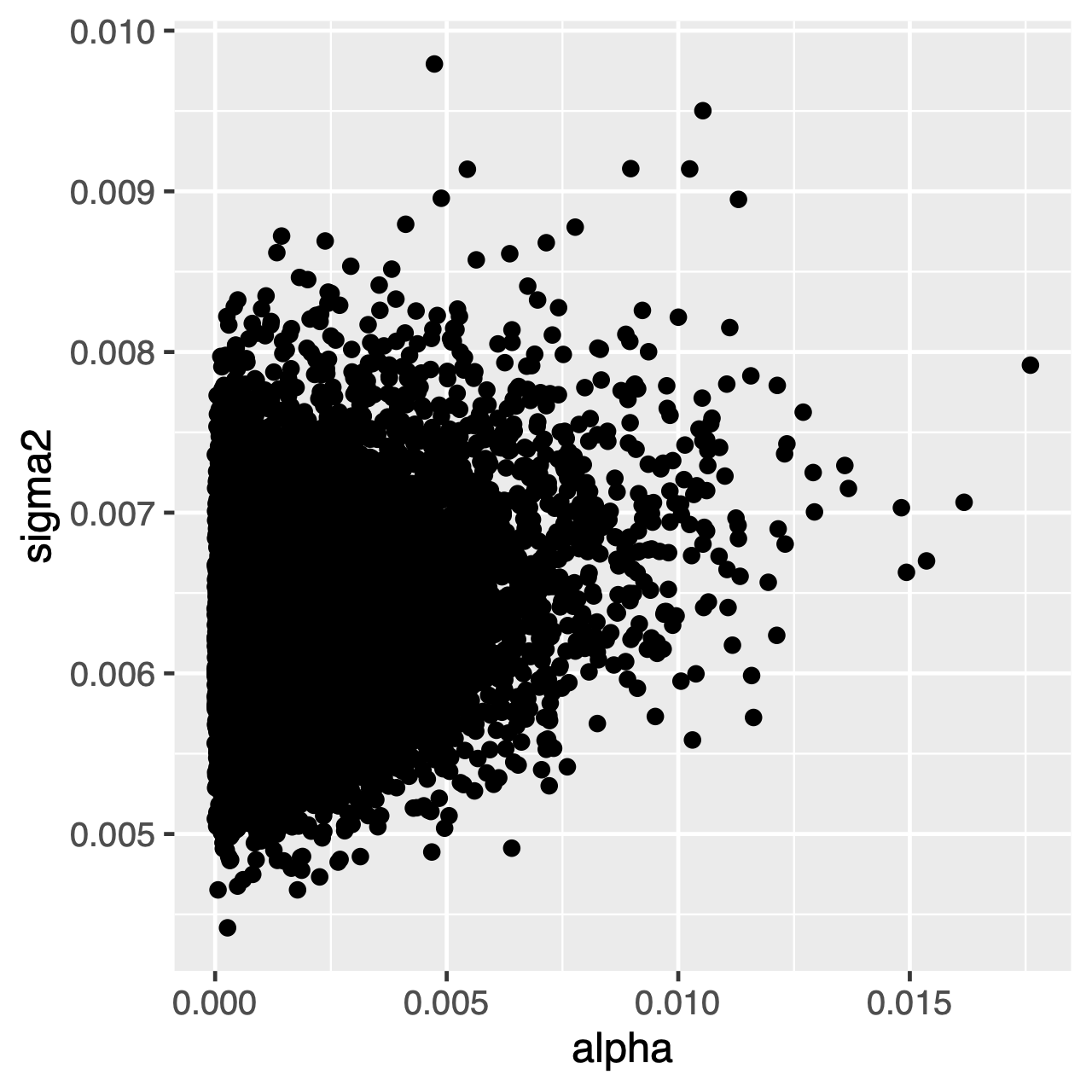
Oefening 1

• voer een MCMC-simulatie uit om de posterieure verdeling van het ou-optimum (theta) te schatten.
• laad het gegenereerde uitvoerbestand in Tracer: Wat is de gemiddelde latere schatting van theta en wat is de geschatte HPD?
• gebruik Tracer om de gezamenlijke posterieure verdeling van alpha en sigma2te vergelijken. Zijn deze parameters gecorreleerd of niet gecorreleerd?
• vergelijk het voorgaand gemiddelde met het achterliggende gemiddelde. (Hint: gebruik het optionele argument underPrior=TRUE in de functie mymcmc.run()) zijn ze verschillend (bijv.)? Is het posterieure gemiddelde buiten het eerdere 95% waarschijnlijkheidsinterval?

het vergelijken van OU-en BM-modellen

nu we zowel BM-als OU-modellen kunnen gebruiken, willen we natuurlijk weten welk model beter past. In deze sectie leren we hoe je reversible-jump Markov chain Monte Carlo kunt gebruiken om de pasvorm van OU-en BM-modellen te vergelijken.

modelselectie met behulp van Reversible-Jump MCMC

om de hypothese te testen dat een karakter evolueert naar een selectief optimum, stellen we ons twee modellen voor. Het eerste model, waarbij er geen aanpassing is naar het optimum, is het geval wanneer $ \ alpha = 0$. Het tweede model komt overeen met het OU-model met $\alpha > 0$. Dit werkt omdat Brownse beweging een speciaal geval is van het OU-model wanneer de snelheid van aanpassing 0 is. Helaas, omdat $\alpha$ een continue parameters is, zal een standaard Markov keten nooit Staten bezoeken waar elke waarde precies gelijk is aan 0. Gelukkig kunnen we reversible jump gebruiken om de Markov-keten te laten overwegen om het Brownse-motion-model te bezoeken. Dit houdt in het specificeren van de eerdere waarschijnlijkheid op elk van de twee modellen, en het verstrekken van de eerdere distributie voor $\alpha$ voor het OU model.

met rjMCMC kan de Markov-keten de twee modellen bezoeken in verhouding tot hun posterieure waarschijnlijkheid. De posterieure waarschijnlijkheid van model $ i$ is gewoon de fractie van monsters waar de keten dat model bezocht. Omdat we ook een prior op de modellen specificeren, kunnen we een Bayes Factor voor het OU model berekenen als:

\

waarbij $P( \text{ou model} \mid X)$ en $P( \text{ou model})$ respectievelijk de posterior probability en de prior probability van het ou model zijn.

Reversible-jump tussen OU-en BM-modellen

om rjMCMC in te schakelen, moeten we gewoon een reversible-jump vooraf plaatsen op de relevante parameter, $\alpha$. We kunnen de prior wijzigen op alpha zodat het ofwel een constante waarde van 0 neemt, ofwel wordt getrokken uit een eerdere distributie. Ten slotte specificeren we een eerdere kans op het OU-model van p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

we bieden dan een reversible-jump voorstel op alpha dat wijzigingen tussen de twee modellen voorstelt.

moves.append( mvRJSwitch(alpha, weight=1.0) )

Daarnaast bieden we het normale mvScale voorstel voor wanneer de MCMC het OU-model bezoekt.

moves.append( mvScale(alpha, weight=1.0) )

we nemen een variabele op die een waarde heeft van 1 wanneer de keten het OU-model bezoekt, en een overeenkomstige variabele die waarde 1 heeft wanneer hij het BM-model bezoekt. Dit zal ons toelaten om gemakkelijk de posterieure waarschijnlijkheid van de modellen te berekenen omdat we gewoon de posterieure gemiddelde waarde van deze parameter moeten berekenen.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

het deel van de monsters waarvoor is_OU = 1 de posterieure waarschijnlijkheid van het OU-model is. Als alternatief komt de gemiddelde schatting achteraf van deze indicatorvariabele overeen met de waarschijnlijkheid achteraf van het OU-model. Deze waarden kunnen worden gebruikt in de Bayes Factor vergelijking hierboven om de Bayes Factor ondersteuning voor elk model te berekenen.

1. Felsenstein J. 1985. Phylogenies and the comparative method. De Amerikaanse Naturalist.:1-15.10.1086/284325
2. Höhna S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. 2014. Probabilistische grafische Modelrepresentatie in Fylogenetica. Systematische Biologie. 63: 753-771. 10. 1093/sysbio / syu039
3. Landis M. J., Schraiber J. G. 2017. Gepulseerde evolutie gevormde moderne gewervelde lichaamsgrootte. Proceedings of the National Academy of Sciences. 114: 13224-13229. 10. 1073/pnas.1710920114