Als u het vorige bericht hebt gelezen over wat een inductor is, laten we doorgaan naar het volgende niveau, Wat is de inductantieformule circuits.
nu de inductor is toegevoegd aan onze lijst van passieve elementen, is het noodzakelijk om het krachtige instrument van serie-parallelle combinatie uit te breiden. We moeten weten hoe we de equivalente inductantie van een serie-aangesloten of parallel-aangesloten set van inductoren te vinden in praktische circuits.
serie smoorspoelen
overweeg een serieaansluiting van n-smoorspoelen, zoals weergegeven in Figuur.(1a), met het equivalente circuit in Figuur.(1 ter).

de inductoren hebben dezelfde stroom door hen. Het toepassen van KVL tot het aansluitnet,

het Vervangen van vk= Lk di/dt resultaten in
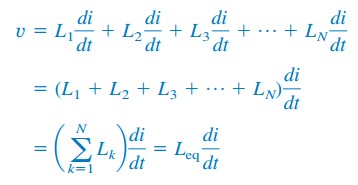
waar

Zo,
De equivalente waarde van serie geschakelde spoelen is de som van de individuele inducties.
smoorspoelen in serie worden op precies dezelfde wijze gecombineerd als weerstanden in serie.
parallelle smoorspoelen
we beschouwen nu een parallelle aansluiting van n-smoorspoelen, zoals weergegeven in Figuur.(2a), met het equivalente circuit in Figuur.2 ter. De inductoren hebben dezelfde spanning over hen. Met behulp van KCL,

Maar


dus

waar
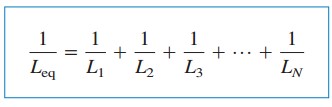
De eerste stroom i(t0) door Leq, t= t0 wordt verwacht door KCL aan de som van de inductor stromingen op t0. Dus, volgens vergelijking.(5),
![]()
volgens de vergelijking.(6),
de equivalente inductie van evenwijdige inductoren is de wederkerigheid van de som van de wederkerigheid van de afzonderlijke inductanties.
de evenwijdige smoorspoelen worden op dezelfde wijze gecombineerd als de evenwijdige weerstanden.
voor twee evenwijdige smoorspoelen (N = 2), vergelijking.(6) wordt
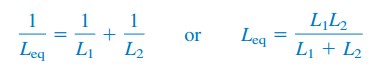
voorbeelden van Inductieformule Circuits
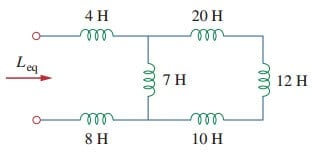
1. Zoek de equivalente inductantie van het circuit in Figuur.(3).
oplossing:
de 10-H -, 12-H-en 20-H-inductoren zijn in serie; de combinatie van deze inductoren geeft dus een 42-h-Inductantie. Deze 42-H-inductor is evenwijdig aan de 7-H-inductor zodat ze gecombineerd worden, zodat


deze 6-h-inductor is in serie met de 4-H-en 8-h-inductoren. Vandaar,
![]()
2. Voor het circuit in Figuur.(4),
i ( t) = 4 (2−e-10t) mA. Als i2(0) = -1 mA, vinden:
(a) i1(0);
(b) v(t), v1(t), en v2(t);
(c) i1(t) en i2(t).

oplossing:
(A) uit i ( t) = 4 (2 − e−10t) mA, i(0) = 4(2 − 1) = 4 mA.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(c) De huidige i1 wordt verkregen als


Ook,


Merk op dat i1(t) + i2(t) = i(t).