Równanie różniczkowe duffinga

najbardziej ogólną formą równania matematycznego jest

(1)

w zależności od wybranych parametrów równanie może przybierać różne formy specjalne. Na przykład, bez tłumienia i bez wymuszania, i biorąc znak plus, równanie staje się

(2)

(Bender i Orszag 1978, s. 547; Zwillinger 1997, s. 122). To równanie może wykazywać chaotyczne zachowanie. Dla równanie oznacza „twardą sprężynę”, a dla oznacza ” miękką sprężynę.”Jeśli , krzywe portret fazy są zamknięte.

jeśli zamiast tego weźmiemy , , zresetujemy zegar tak, aby i użyjemy znaku minus, równanie jest wtedy

(3)

można to zapisać jako układ równań różniczkowych zwyczajnych pierwszego rzędu jako

			(4)
			(5)

(Wiggins 1990, s. 5), który w niewymuszonym przypadku zmniejsza się do

			(6)
			(7)

(Wiggins 1990, s. 6; Ott 1993, s. 3).

PUNKTY STAŁE tego zbioru sprzężonych równań różniczkowych są podane przez

(8)

so , oraz

			(9)
			(10)

daje . PUNKTY STAŁE są więc, , oraz .

Analiza stabilności punktów stałych może być punktowa poprzez linearyzację równań. Różnicowanie daje

			(11)
			(12)
			(13)

które można zapisać jako równanie macierzowe

(14)

badanie stabilności punktu (0,0):

(15)

(16)

ale , więc jest prawdziwe. Ponieważ , zawsze będzie jeden dodatni pierwiastek, więc ten stały punkt jest niestabilny. Teraz spójrz na (, 0). Równanie charakterystyczne to

(17)

która ma korzenie

(18)

dla, , więc punkt jest asymptotycznie stabilny. If , , więc punkt jest liniowo stabilny (Wiggins 1990, str. 10). Jeśli jednak , pierwiastek daje część urojoną, a część rzeczywista jest , więc punkt jest niestabilny. If , , który ma dodatni pierwiastek rzeczywisty, więc punkt jest niestabilny. Jeśli, to, więc oba pierwiastki są dodatnie, a punkt jest niestabilny.

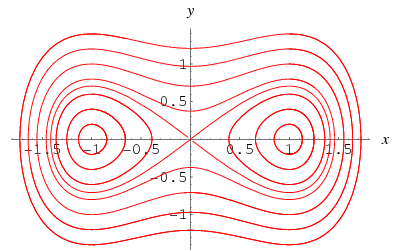
co ciekawe szczególny przypadek bez wymuszania,

			(19)
			(20)

może być zintegrowany za pomocą kwadratów. Różnicowanie (19) i pluggingin (20) daje

(21)

mnożenie obu stron przez daje

(22)

ale to można napisać

(23)

mamy więc niezmiennik ruchu ,

(24)

rozwiązywanie dla daje

(25)

(26)

so

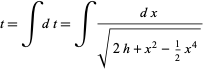(27)

(Wiggins 1990, p. 29).

Note that the invariant of motion satisfies

(28)

(29)

więc równania oscylatora Duffinga są podane przez Hamiltonianów