funkcja konsumpcji keynesowskiej opierała się na dwóch głównych hipotezach. Po pierwsze, marginalna skłonność do konsumpcji mieści się między 0 a 1. Po drugie, średnia skłonność do konsumpcji spada wraz ze wzrostem dochodów. Wczesne badania empiryczne były zgodne z tymi hipotezami. Jednak po ii wojnie światowej zauważono, że oszczędzanie nie rosło wraz ze wzrostem dochodów. W związku z tym Model Keynesowski nie wyjaśnił zjawiska konsumpcji, w związku z czym powstała teoria wyboru międzyczasowego. Analizę wyboru intertemporalnego wprowadził John Rae w 1834 roku w „socjologicznej teorii kapitału”. Później nad modelem pracowali Eugen von Böhm-Bawerk w 1889 i Irving Fisher w 1930. Kilka innych modeli opartych na wyborze intertemporalnym to hipoteza cyklu życia zaproponowana przez Franco Modiglianiego i hipoteza stałego dochodu zaproponowana przez Miltona Friedmana. Pojęcie równowagi Walrasyjskiej może być również rozszerzone o wybór międzyczasowy. Walrasiańska analiza takiej równowagi wprowadza dwie „nowe” koncepcje cen: ceny kontraktów terminowych i ceny spot.
Model spożycia międzyczasuedytuj
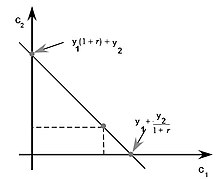

Irving Fisher rozwinął teorię wyboru intertemporalnego w swojej książce Theory of interest (1930). W przeciwieństwie do Keynesa, który powiązał konsumpcję z bieżącymi dochodami, Model Fishera pokazał, jak racjonalnie wybierają konsumpcję na teraźniejszość i przyszłość, aby zmaksymalizować satysfakcję z życia.
według Fishera niecierpliwość jednostki zależy od czterech cech jego strumienia dochodów: wielkości, kształtu czasu, składu i ryzyka. Poza tym przewidywanie, samokontrola, nawyk, oczekiwanie na życie i motyw spadkowy (lub troska o życie innych) są pięcioma osobistymi czynnikami, które determinują niecierpliwość osoby, która z kolei determinuje jej preferencje czasowe.
aby zrozumieć wybór dokonywany przez konsumenta w różnych okresach, traktujemy konsumpcję w jednym okresie jako towar złożony. Załóżmy, że istnieje jeden konsument, N {\displaystyle N}

i dwa okresy. Preferencje są określone przez U ( x 1 , x 2 ) {\styl wyświetlania U(x_{1}, x_{2})}

gdzie x t = (x T 1,… , x t n ) {\styl wyświetlania x_{t}=(x_{T1},\punkty,x_{TN})}

. Przychody za okres t {\styl wyświetlania t}

poniżej znajduje się t {\styl wyświetlania Y_{t}}

. Oszczędności w okresie 1 to S 1 {\displaystyle S_{1}}

, wydatki w okresie t {\displaystyle t}

is C T {\displaystyle C_{t}}

, and r {\displaystyle r}

to stopa procentowa. Jeśli dana osoba nie jest w stanie zaciągnąć pożyczki na poczet przyszłych dochodów w pierwszym okresie, podlega ona odrębnym ograniczeniom budżetowym w każdym okresie: C 1 + S 1 ≤ Y 1, {\displaystyle C_{1} + s_{1} \ leq Y_{1},}

(1) C 2 ≤ Y 2 + S 1 ( 1 + r). {\displaystyle C_{2} \ leq Y_{2} + S_{1} (1+r).}

(2)
z drugiej strony, jeśli takie zaciągnięcie pożyczki jest możliwe, osoba podlega jednemu międzyokresowemu ograniczeniu budżetowemu:
C 1 + C 2 1 + R = Y 1 + Y 2 1 + r . {\displaystyle C_ {1}+{\frac{C_{2}} {1+r}}=Y_ {1}+{\frac{Y_{2}} {1+r}}.

(3)
lewa strona pokazuje aktualną wartość wydatków, a prawa strona przedstawia aktualną wartość dochodów. Mnożenie równania przez (1 + r ) {\displaystyle (1 + r)}

dałoby nam odpowiednie przyszłe wartości.
teraz konsument musi wybrać C 1 {\displaystyle C_{1}}

i C 2 {\displaystyle C_{2}}

aby zmaksymalizować U (C 1, C 2) {\displaystyle U (C_{1}, C_{2})}

z zastrzeżeniem C 1 + C 2 / (1 + r ) = Y 1 + Y 2 / (1 + r ) . {\displaystyle C_{1} + C_{2}/(1+r)=Y_{1}+Y_{2} / (1 + r).}



konsument może być oszczędzającym netto lub kredytobiorcą netto. Jeśli początkowo jest na poziomie konsumpcji, w którym nie jest ani pożyczkobiorcą netto, ani oszczędzającym netto, wzrost dochodu może uczynić go oszczędzającym netto lub pożyczkobiorcą netto w zależności od jego preferencji. Wzrost bieżących dochodów lub przyszłych dochodów zwiększy bieżącą i przyszłą konsumpcję (motywy wygładzania konsumpcji).
teraz rozważmy scenariusz, w którym stopy procentowe zostaną podwyższone. Jeśli konsument jest oszczędzającym netto, zaoszczędzi więcej w bieżącym okresie ze względu na efekt substytucji i zużyje więcej w bieżącym okresie ze względu na efekt dochodowy. Efekt sieci staje się więc niejednoznaczny. Jeśli jednak konsument jest kredytobiorcą netto, będzie miał tendencję do spożywania mniej w bieżącym okresie ze względu na efekt substytucji i efekt dochodowy, zmniejszając w ten sposób jego ogólne zużycie bieżące.
hipoteza dochodu w cyklu Życiowymedytuj
hipoteza cyklu życia opiera się na następującym modelu:
max U T = ∑ T U ( C t ) ( 1 + δ ) − t {\displaystyle \max u_{t}=\sum _{T}U(C_{t})(1+\delta )^{-t}}

subject to
∑ T C T ( 1 + r) − T = ∑ T Y T ( 1 + r) – T + w 0 , {\displaystyle \sum _{t}C_{t}(1+r)^{- t} = \sum _{t} Y_{t}(1+R)^{-t}+W_{0},}

gdzie
U (Ct) to zadowolenie z konsumpcji w okresie t, Ct to poziom konsumpcji w czasie t, Yt to dochód w czasie T, δ to szybkość czasu preferencja (miara indywidualnej preferencji pomiędzy bieżącą i przyszłą działalnością), W0 to początkowy poziom aktywów generujących dochód.

zazwyczaj RPP (marginalna skłonność do konsumpcji) jest stosunkowo wysoka w młodym wieku, zmniejsza się w wieku średnim i wzrasta, gdy osoba jest w pobliżu lub na emeryturze. Model Life Cycle Hypothesis(LCH) definiuje indywidualne zachowanie jako próbę wygładzenia wzorców konsumpcji w ciągu swojego życia, w sposób nieco niezależny od obecnego poziomu dochodów. Model ten stwierdza, że na początku życia wydatki konsumpcyjne mogą bardzo dobrze przekraczać dochody, ponieważ jednostka może dokonywać dużych zakupów związanych z zakupem nowego domu, zakładaniem rodziny i rozpoczynaniem kariery. Na tym etapie życia jednostka będzie pożyczać z przyszłości, aby wspierać te potrzeby wydatków. Jednak w połowie życia te schematy wydatków zaczynają się wyrównywać i są wspierane lub być może przekraczane przez wzrost income.At na tym etapie Jednostka spłaca wszelkie wcześniejsze pożyczki i zaczyna oszczędzać na swoją emeryturę.Po przejściu na emeryturę wydatki konsumpcyjne mogą zacząć spadać, jednak dochody Zwykle dramatycznie spadają. Na tym etapie życia jednostka nie oszczędza lub żyje z wcześniejszych oszczędności aż do śmierci.
hipoteza o stałym dochodzie Friedmanaedytuj
po ii wojnie światowej zauważono, że model, w którym bieżąca konsumpcja była tylko funkcją bieżących dochodów, był wyraźnie zbyt uproszczony. Nie można było wyjaśnić faktu, że długoterminowa średnia skłonność do konsumpcji wydawała się być z grubsza stała, mimo że marginalna skłonność do konsumpcji jest znacznie niższa. Tak więc hipoteza stałego dochodu Miltona Friedmana jest jednym z modeli, który stara się wyjaśnić tę pozorną sprzeczność.
zgodnie z hipotezą stałego dochodu, stała konsumpcja, CP, jest proporcjonalna do stałego dochodu, YP. Stały dochód jest subiektywnym pojęciem prawdopodobnego średniego przyszłego dochodu. Konsumpcja stała jest podobnym pojęciem konsumpcji.
rzeczywiste zużycie, C, i rzeczywisty dochód, Y, składają się z tych stałych składników plus nieprzewidziane składniki przejściowe, CT i yt, odpowiednio:
CPt =ß2YPt Ct = CPt + CTt Yt = YPt + YTt