- Estimar optima sob Ornstein-Uhlenbeck evolução Michael R. Pode Última modificação em setembro 16, 2019
- A estimativa Evolutiva Optima
- Ornstein-Uhlenbeck Model
- leia os dados
- especificando o modelo
- modelo de árvore
- parâmetro da taxa
- parâmetro de Adaptação
- Optimum
- Ornstein-Uhlenbeck modelo
- Executando uma MCMC análise de Especificando Monitores Para o nosso MCMC análise, precisamos definir um vetor de monitores para gravar os estados de nossa cadeia de Markov. As funções de monitor são todas chamadas mn*, onde * é a placa que representa o tipo de monitor. Primeiro, inicializaremos o monitor modelo usando a função mnModel. Isto cria uma nova variável de monitor que irá produzir os estados para todos os parâmetros do modelo quando passados em uma função MCMC. monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) ) além disso, crie um monitor de tela que relatará os estados de variáveis específicas para a tela com mnScreen: monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) ) Inicializar e Executar a Simulação MCMC Com o modelo especificado um conjunto de monitores, e um conjunto de movimentos, wecan agora configurar o algoritmo MCMC que irá exemplo de valores de parâmetro inproportion para sua posterior de probabilidade. O mcmc() função willcreate nosso MCMC objeto: mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed") Agora, execute o MCMC: mymcmc.run(generations=50000) Quando a análise for concluída, você terá os arquivos monitorados em youroutput directory. ⇨ o ficheiro Rev para a realização desta análise: mcmc_OU.Rev os caracteres que evoluem sob o processo OU tenderão para uma distribuição estacionária,que é uma distribuição normal com média $\theta$ e variância $ \ sigma^2 \div 2 \ alpha$. Portanto, se as taxas de evolução são altas (ou os ramos na árvore são relativamente longos), pode ser difícil estimar $\sigma^2$ e $\alpha$ separadamente, uma vez que ambos determinam a variância de longo prazo do processo. Podemos ver se isso afeta nossa análise examinando a distribuição posterior conjunta dos parâmetros em Tracer. Quando os parâmetros estão positivamente correlacionados, devemos hesitar em interpretar suas distribuições marginais (ou seja, não fazer inferências sobre a taxa de adaptação ou o parâmetro de variância separadamente). estimativas da distribuição posterior conjunta da taxa de adaptação, $\alpha$ (eixo x), e o parâmetro de variância, $\sigma^2$ (eixo y). Note que estes parâmetros estão positivamente correlacionados. Exercício 1
- comparando os modelos OU E BM
- seleção de modelos usando MCMC de Salto reversível
- Reversible-jump between OU and BM models
Estimar optima sob Ornstein-Uhlenbeck evolução
Michael R. Pode
Última modificação em setembro 16, 2019
A estimativa Evolutiva Optima
Este tutorial demonstra como especificar um Ornstein-Uhlenbeck modelo onde o ideal fenótipo é assumida ser constante entre os galhos de uma vez calibrado, filogenia (falta de referência) utilizando os conjuntos de dados (log) do corpo-de tamanho através de vertebrados subtipos de (falta de referência). Nós fornecemos a representação probabilística do modelo gráfico de cada componente para este tutorial. Depois de especificar o modelo, você irá estimar os parâmetros da evolução Ornstein-Uhlenbeck usando a cadeia Markov Monte Carlo (MCMC).
Ornstein-Uhlenbeck Model
Under the simple Ornstein-Uhlenbeck (OU) model, a continuous character is assumed to evolve towards an optimal value, $\theta$. O personagem evolui estocasticamente de acordo com um parâmetro drift, $\sigma^2$. O personagem é puxado para o melhor pela taxa de adaptação, $\alpha$; valores maiores de alpha indicam que o personagem é puxado mais fortemente para $\theta$. À medida que o personagem se afasta de $\theta$, o parâmetro $\alpha$ determina a força com que o personagem é puxado para trás. Por esta razão, $\alpha$ é por vezes referido como um parâmetro de “banda de borracha”. Quando a taxa de adaptação do parâmetro $\alpha = 0$, o modelo OU colapsa para o modelo BM. O modelo gráfico resultante é bastante simples, pois a probabilidade dos caracteres contínuos depende apenas da filogenia (que assumimos ser conhecida neste tutorial) e do parâmetro OU ().
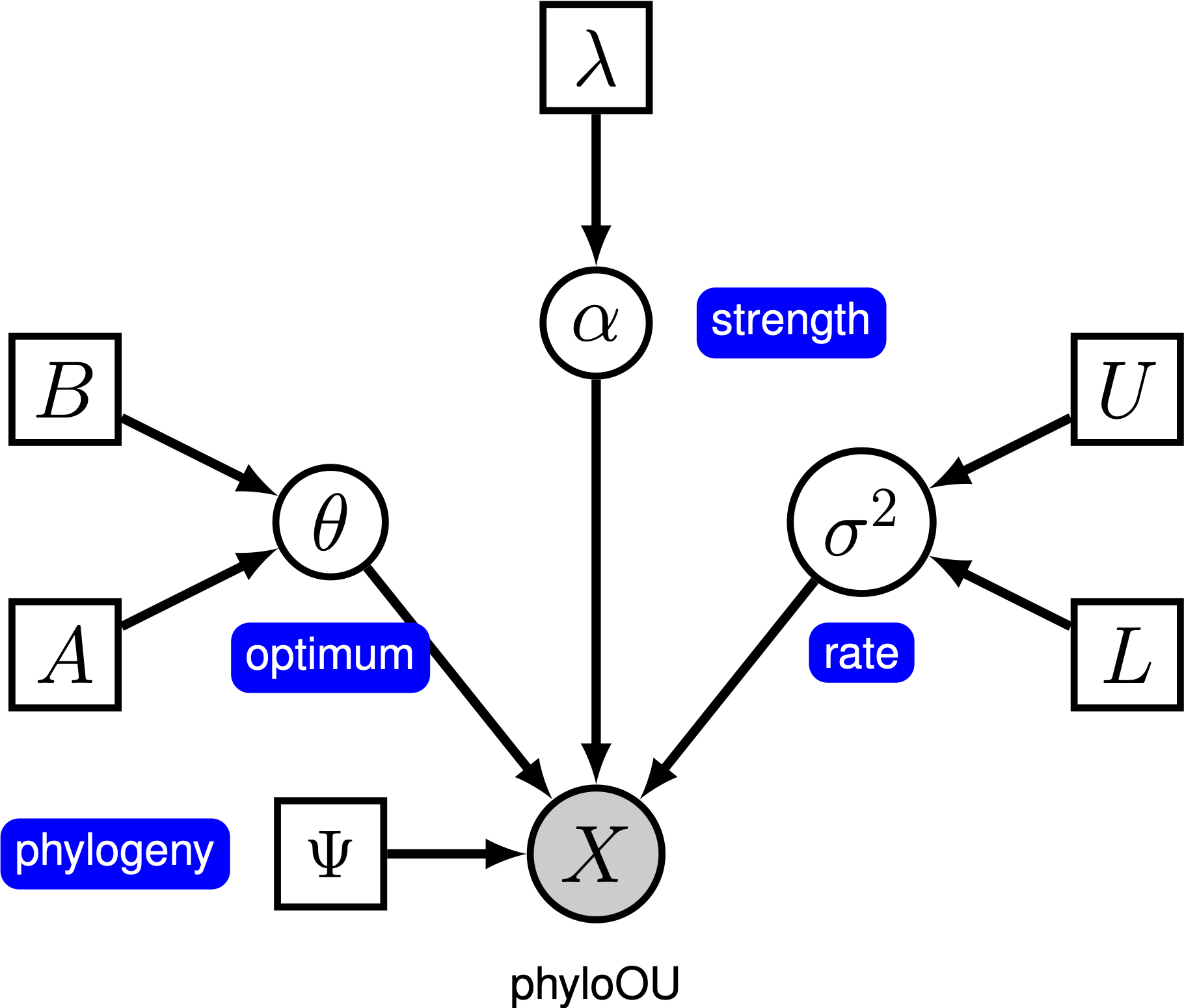
In this tutorial, we use the 66 vertebrate phylogenies and (log) body-size datasets from (Landis and Schraiber 2017).
⇨ a especificação completa OU-model está no arquivo chamado mcmc_OU.Rev.
leia os dados
começamos por decidir qual dos 66 conjuntos de dados vertebrados usar. Aqui, assumimos que estamos analisando o primeiro conjunto de dados (Acanthuridae), mas você deve se sentir livre para escolher qualquer um dos conjuntos de dados.
dataset <- 1agora, nós lemos na árvore (calibrada no tempo) correspondente ao nosso conjunto de dados escolhido.
T <- readTrees("data/trees.nex")em seguida, nós lemos nos dados de caráter para o mesmo conjunto de dados.
data <- readContinuousCharacterData("data/traits.nex")além disso, inicializamos uma variável para nosso Vetor de móves e monitores:
moves = VectorMoves()monitors = VectorMonitors()especificando o modelo
modelo de árvore
neste tutorial, assumimos que a árvore é conhecida sem área. Nós criamos um nó constante para a árvore que corresponde à filogenia observada.
tree <- Tparâmetro da taxa
a taxa estocástica de evolução é controlada pelo parâmetro da taxa, $\sigma^2$. Nós desenhamos o parâmetro da taxa de um prior loguniforme. Este prior é uniforme na escala log, o que significa que representa ignorância sobre a ordem de magnitude da taxa.
sigma2 ~ dnLoguniform(1e-3, 1)a fim de estimar a distribuição posterior de $ \sigma^2$, devemos fornecer um mecanismo de proposta MCMC que opera neste nó. Porque $\sigma^2$ é um parâmetro de taxa, e deve, portanto, ser positivo, nós usamos um movimento de escala chamado mvScale.
moves.append( mvScale(sigma2, weight=1.0) )parâmetro de Adaptação
A taxa de adaptação para o ótimo é determinado pelo parâmetro $\alpha$. Nós tiramos $ \alpha$ de uma distribuição exponencial anterior, e colocar uma proposta de escala sobre ele.
alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )Optimum
desenhamos o valor óptimo a partir de um vago uniforme antes que varie de -10 a 10 (deve alterar este anterior se o seu carácter estiver fora deste intervalo). Como este parâmetro pode ser positivo ou negativo, usamos um slide para propor alterações durante o MCMC.
theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )Ornstein-Uhlenbeck modelo
Agora que temos especificou os parâmetros do modelo, podemos desenhar o personagem de dados a partir do correspondente filogenética modelo de UO. Neste exemplo, usamos o algoritmo REML para calcular eficientemente a probabilidade (Felsenstein 1985). Assumimos que o personagem começa no valor ideal na raiz da árvore.
X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)notando que $X$ é os dados observados (), nós grampeamos o data para este nó estocástico.
X.clamp(data)finalmente, criamos um objeto de espaço de trabalho para todo o modelo com model(). Remeber que objetos de espaço de trabalho são inicializados com o operador =, e não são eles mesmos parte do modelo gráfico Bayesiano. A função model() atravessa todo o grafo modelo e encontra todos os nós no modelo que especificamos. Este objeto fornece uma maneira conveniente de se referir a todo o objeto modelo, ao invés de apenas um único nó DAG.
mymodel = model(theta)Executando uma MCMC análise de
Especificando Monitores
Para o nosso MCMC análise, precisamos definir um vetor de monitores para gravar os estados de nossa cadeia de Markov. As funções de monitor são todas chamadas mn*, onde * é a placa que representa o tipo de monitor. Primeiro, inicializaremos o monitor modelo usando a função mnModel. Isto cria uma nova variável de monitor que irá produzir os estados para todos os parâmetros do modelo quando passados em uma função MCMC.
monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )
além disso, crie um monitor de tela que relatará os estados de variáveis específicas para a tela com mnScreen:
monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )
Inicializar e Executar a Simulação MCMC
Com o modelo especificado um conjunto de monitores, e um conjunto de movimentos, wecan agora configurar o algoritmo MCMC que irá exemplo de valores de parâmetro inproportion para sua posterior de probabilidade. O mcmc() função willcreate nosso MCMC objeto:
mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")
Agora, execute o MCMC:
mymcmc.run(generations=50000)
Quando a análise for concluída, você terá os arquivos monitorados em youroutput directory.
⇨ o ficheiro Rev para a realização desta análise: mcmc_OU.Rev
os caracteres que evoluem sob o processo OU tenderão para uma distribuição estacionária,que é uma distribuição normal com média $\theta$ e variância $ \ sigma^2 \div 2 \ alpha$. Portanto, se as taxas de evolução são altas (ou os ramos na árvore são relativamente longos), pode ser difícil estimar $\sigma^2$ e $\alpha$ separadamente, uma vez que ambos determinam a variância de longo prazo do processo. Podemos ver se isso afeta nossa análise examinando a distribuição posterior conjunta dos parâmetros em Tracer. Quando os parâmetros estão positivamente correlacionados, devemos hesitar em interpretar suas distribuições marginais (ou seja, não fazer inferências sobre a taxa de adaptação ou o parâmetro de variância separadamente).
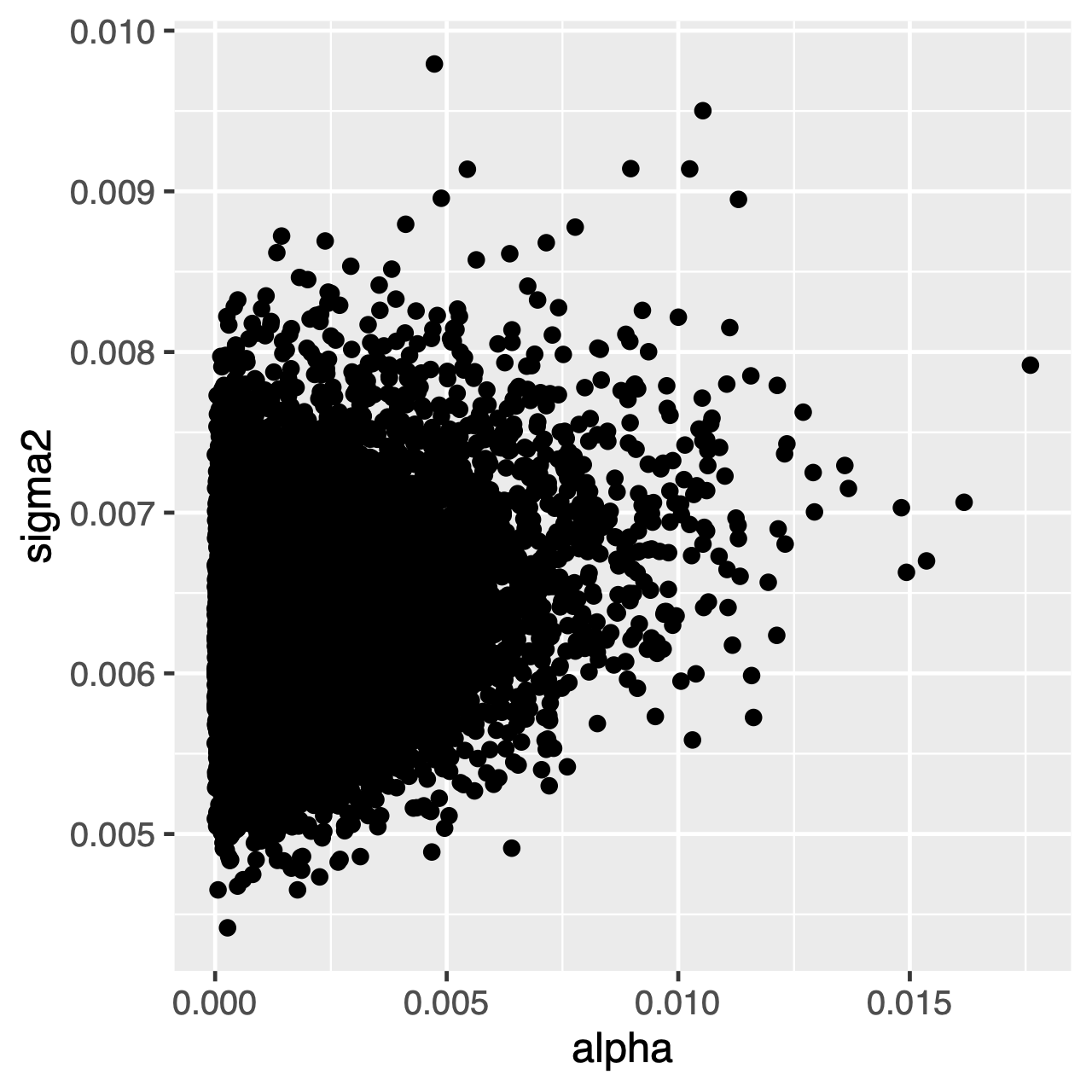
estimativas da distribuição posterior conjunta da taxa de adaptação, $\alpha$ (eixo x), e o parâmetro de variância, $\sigma^2$ (eixo y). Note que estes parâmetros estão positivamente correlacionados.
Exercício 1
- execute uma simulação MCMC para estimar a distribuição posterior do OU optimum (
theta).
- carregar o ficheiro de saída gerado em
Tracer: Qual é a estimativa posterior média de theta e qual é a estimativa HPD?
- Use
Tracer para comparar as distribuições posteriores conjuntas de alpha e sigma2. Estes parâmetros estão correlacionados ou não correlacionados?
- Compare a média anterior com a média posterior. (DICA: Use o argumento opcional
underPrior=TRUE na função mymcmc.run()) eles são diferentes (por exemplo, )? A média posterior está fora do intervalo de probabilidade de 95%?
comparando os modelos OU E BM
agora que podemos encaixar ambos os modelos BM E OU, podemos naturalmente querer saber que modelo se encaixa melhor. Nesta seção, aprenderemos a usar a cadeia de salto reversível Monte Carlo para comparar o ajuste dos modelos OU E BM.
seleção de modelos usando MCMC de Salto reversível
para testar a hipótese de que um personagem evolui para um ideal seletivo, imaginamos dois modelos. O primeiro modelo, onde não há adaptação para o ideal, é o caso quando $\alpha = 0$. O segundo modelo corresponde ao modelo OU com $ \alpha > 0$. Isto funciona porque o movimento browniano é um caso especial do modelo OU quando a taxa de adaptação é 0. Infelizmente, porque $\alpha$ é um parâmetro contínuo, uma cadeia padrão Markov nunca irá visitar estados onde cada valor é exatamente igual a 0. Felizmente, podemos usar o salto reversível para permitir que a cadeia Markov considere visitar o modelo de movimento browniano. Isso envolve especificar a probabilidade anterior em cada um dos dois modelos, e fornecer a distribuição anterior de $\alpha$ para o modelo OU.
usando rjMCMC permite que a cadeia Markov visite os dois modelos em proporção à sua probabilidade posterior. A probabilidade posterior do modelo $I$ é simplesmente a fração de amostras onde a cadeia estava visitando esse modelo. Como também especificamos um prior nos modelos, podemos calcular um fator Bayes para o modelo OU como:
\
onde $P (\text{ou model} \ mid X)$ E $P (\text{OU model})$ são a probabilidade posterior e a probabilidade anterior do modelo OU, respectivamente.
Reversible-jump between OU and BM models
To enable rjMCMC, we simply have to place a reversible-jump prior on the relevant parameter, $\alpha$. Nós podemos modificar o prior em alpha de modo que ele leva um valor constante de 0, ou é desenhado a partir de uma distribuição anterior. Finalmente, especificamos uma probabilidade anterior no modelo OU de p = 0.5.
alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)
nós então fornecemos uma proposta reversível de salto em alpha que propõe mudanças entre os dois modelos.
moves.append( mvRJSwitch(alpha, weight=1.0) )
além disso, nós fornecemos a proposta normal mvScale para quando o MCMC está visitando o modelo OU.
moves.append( mvScale(alpha, weight=1.0) )
nós incluímos uma variável que tem um valor 1 quando a cadeia está visitando o modelo OU, e uma variável correspondente que tem valor 1 quando está visitando o modelo BM. Isso nos permitirá calcular facilmente a probabilidade posterior dos modelos, porque simplesmente precisamos calcular o valor médio posterior deste parâmetro.
is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)
a fracção de amostras para a qual is_OU = 1 é a probabilidade posterior do modelo OU. Alternativamente, a estimativa média posterior desta variável indicadora corresponde à probabilidade posterior do modelo OU. Estes valores podem ser usados na equação do fator de Bayes acima para calcular o suporte do fator de Bayes para qualquer modelo.
- Felsenstein J. 1985. Phylogenies and the comparative method. O Naturalista Americano.:1-15.10.1086/284325
- Höhna S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. De 2014. Probabilistic Graphical Model Representation in Phylogenetics. Biologia Sistemática. 63:753-771.10.1093/sysbio/syu039
- Landis M. J., Schraiber J. G. de 2017. Evolução pulsada moldou o tamanho moderno do corpo vertebrado. Proceedings of the National Academy of Sciences. 114: 13224-13229. 10. 1073 / pnas.1710920114
mn*, onde * é a placa que representa o tipo de monitor. Primeiro, inicializaremos o monitor modelo usando a função mnModel. Isto cria uma nova variável de monitor que irá produzir os estados para todos os parâmetros do modelo quando passados em uma função MCMC.monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )mnScreen:monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )mcmc() função willcreate nosso MCMC objeto:mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")mymcmc.run(generations=50000)Rev para a realização desta análise: mcmc_OU.RevTracer. Quando os parâmetros estão positivamente correlacionados, devemos hesitar em interpretar suas distribuições marginais (ou seja, não fazer inferências sobre a taxa de adaptação ou o parâmetro de variância separadamente).
theta).Tracer: Qual é a estimativa posterior média de theta e qual é a estimativa HPD?Tracer para comparar as distribuições posteriores conjuntas de alpha e sigma2. Estes parâmetros estão correlacionados ou não correlacionados?underPrior=TRUE na função mymcmc.run()) eles são diferentes (por exemplo, )? A média posterior está fora do intervalo de probabilidade de 95%?alpha de modo que ele leva um valor constante de 0, ou é desenhado a partir de uma distribuição anterior. Finalmente, especificamos uma probabilidade anterior no modelo OU de p = 0.5.alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)alpha que propõe mudanças entre os dois modelos.moves.append( mvRJSwitch(alpha, weight=1.0) )mvScale para quando o MCMC está visitando o modelo OU.moves.append( mvScale(alpha, weight=1.0) )1 quando a cadeia está visitando o modelo OU, e uma variável correspondente que tem valor 1 quando está visitando o modelo BM. Isso nos permitirá calcular facilmente a probabilidade posterior dos modelos, porque simplesmente precisamos calcular o valor médio posterior deste parâmetro.is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)is_OU = 1 é a probabilidade posterior do modelo OU. Alternativamente, a estimativa média posterior desta variável indicadora corresponde à probabilidade posterior do modelo OU. Estes valores podem ser usados na equação do fator de Bayes acima para calcular o suporte do fator de Bayes para qualquer modelo.