Articles

Ecuația diferențială Duffing

author
2 Min Read

descărcați Notebook-ul Mathematica

cea mai generală formă forțată a ecuației Duffing este

x^..+ deltax^.+(betax^3+ / - omega_0^2x) = gammacos(omegat+phi).
(1)

în funcție de parametrii aleși, ecuația poate lua o serie de forme speciale. De exemplu, fără amortizare și fără forțare, delta = gamma = 0 și luând semnul plus, ecuația devine

x^..+ omega_0 ^ 2x + betax^3=0
(2)

(Bender și Orszag 1978, p. 547; Zwillinger 1997, p. 122). Această ecuație poate afișa un comportament haotic. Pentru beta0 , ecuația reprezintă un „arc dur”, iar pentru beta0, reprezintă un ” arc moale.”Dacă beta0 , curbele portret de fază sunt închise.

dacă în schimb luăm beta=1 , omega_0 = 1 , resetați ceasul astfel încât phi = 0 și folosiți semnul minus, ecuația este apoi

x^..+ deltax^.+(x^3-x) = gammacos(omegat).
(3)

acest lucru poate fi scris ca un sistem de ecuații diferențiale ordinare de ordinul întâi ca

x^. = y,
(4)
i^. = x-x^3-deltay + gammacos(omegat)
(5)

(Wiggins 1990, p. 5) care, în cazul neforțat, se reduce la

x^. = y
(6)
i^. = x-x^3-deltay
(7)

(Wiggins 1990, p. 6; Ott 1993, p.3).

punctele fixe ale acestui set de ecuații diferențiale cuplate sunt date de

x^.= y=0,
(8)

deci y = 0 , și

i^. = x-x^3-deltay
(9)
= x (1-x^2)-0
(10)

acordarea x=0,+/-1. Prin urmare, punctele fixe sunt (-1,0), (0,0), și (1,0).

analiza stabilității punctelor fixe poate fi punct prin liniarizarea ecuațiilor. Diferențierea dă

x^.. = i^.
(11)
= x-x^3-deltay
(12)
i^.. = (1-3x^2) x^.- deltay^.,
(13)

care poate fi scris ca ecuația matricei

=.
(14)

examinarea stabilității punctului (0,0):

|0-lambda 1; 1-delta-lambda/ = lambda (lambda+delta)-1 = lambda^2 + lambdadelta-1=0
(15)
lambda_+/-^((0,0))=1/2(-delta + / - sqrt (delta^2 + 4)).
(16)

dar delta ^ 2 = 0 , deci lambda_+/-^((0,0)) este real. Deoarece sqrt (delta^2+4)|delta|, va exista întotdeauna o rădăcină pozitivă, deci acest punct fix este instabil. Acum uita-te la (+/-1, 0). Ecuația caracteristică este

|0-lambda 1; -2-delta-lambda/ = lambda(lambda + delta) + 2 = lambda^2 + lambdadelta+2=0,
(17)

care are rădăcini

lambda_+/-^((+/-1,0))=1/2(-delta + / - sqrt (delta^2-8)).
(18)

pentru delta0 , R0, deci punctul este asimptotic stabil. Dacă delta = 0 , lambda_+/-^((+/-1,0))=+/-isqrt (2), deci punctul este liniar stabil (Wiggins 1990, p. 10). Cu toate acestea, dacă delta în (- 2sqrt(2),0), radicalul dă o parte imaginară, iar partea reală este 0, deci punctul este instabil. Dacă delta = - 2sqrt(2), lambda_+/-^((+/-1,0))=sqrt (2), care are o rădăcină reală pozitivă, deci punctul este instabil. Dacă delta-2sqrt(2) , atunci|delta|sqrt (delta^2-8) , deci ambele rădăcini sunt pozitive și punctul este instabil.

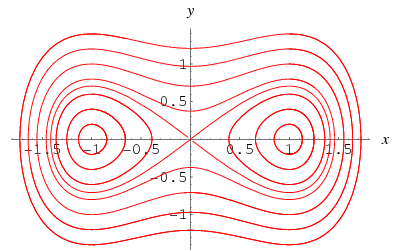
DuffingOscillatorPhasePortrait

interesant, cazul special delta = 0 fără forțare,

x^. = y
(19)
i^. = x-x^3,
(20)

poate fi integrat prin cvadraturi. Diferențierea (19) și conectarea (20) dă

x^..= y^.= x-x^3.
(21)

înmulțirea ambelor părți cu x^. da

x^..x^.- x^.x + x^.x^3=0.
(22)

dar acest lucru poate fi scris

d/(dt) (1 / 2x^.^2-1 / 2x^2 + 1 / 4x^4)=0,
(23)

deci avem un invariant al mișcării h,

h=1 / 2x^.^2-1 / 2x^2+1/4x^4.
(24)

rezolvarea pentru x^.^2 dă

x^.^2=((dx)/(dt))^2=2h+x^2-1/2x^4
(25)
(dx)/(dt)=sqrt(2h+x^2-1/2x^4),
(26)

so

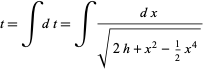t=intdt=int(dx)/(sqrt(2h+x^2-1/2x^4))
(27)

(Wiggins 1990, p. 29).

Note that the invariant of motion h satisfies

x^.=(partialh)/(partialx^.) =(partialh)/(partialy)
(28)
(partialh)/(partialx)= - x + x^3 = - y^.,
(29)

deci ecuațiile oscilatorului Duffing sunt date de Hamiltoniansystem

You might also like

Lasă un răspuns

Adresa ta de email nu va fi publicată.