om du har läst föregående inlägg om vad som är en induktor, låt oss gå vidare till nästa nivå, Vad är induktansformelkretsarna.
nu när induktorn har lagts till i vår lista över passiva element är det nödvändigt att utöka det kraftfulla verktyget för serieparallell kombination. Vi behöver veta hur man hittar motsvarande induktans hos en serieansluten eller parallellansluten uppsättning induktorer som finns i praktiska kretsar.
serie induktorer
Tänk på en serieanslutning av n induktorer, som visas i Figur.(1a), med motsvarande krets som visas i Figur.(1b).

induktorerna har samma ström genom dem. Applicera KVL på slingan,

att ersätta vk= Lk di / dt resulterar i
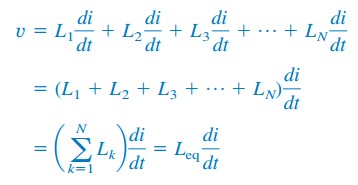
där

således,
den ekvivalenta induktansen hos seriekopplade induktorer är summan av de enskilda induktanserna.
induktorer i serie kombineras på exakt samma sätt som motstånd i serie.
parallella induktorer
vi betraktar nu en parallell anslutning av n induktorer, som visas i Figur.(2a), med motsvarande krets i Figur.(2b). Induktorerna har samma spänning över dem. Använda KCl,

men


därför

där
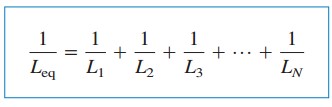
den initiala strömmen i (t0) genom Leq vid t= t0 förväntas av KCL vara summan av induktorströmmarna vid t0. Således enligt ekvation.(5),
![]()
enligt ekvation.(6),
den ekvivalenta induktansen hos parallella induktorer är det ömsesidiga av summan av de enskilda induktansernas reciprokaler.
Observera att induktorerna parallellt kombineras på samma sätt som motstånd parallellt.
för två induktorer parallellt (N = 2), ekvation.(6) blir
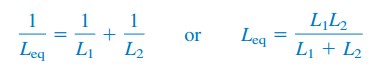
induktans formel kretsar exempel
1. Hitta motsvarande induktans för kretsen som visas i Figur.(3).
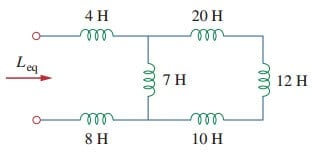
lösning:
induktorerna 10-H, 12-H och 20-h är i serie; således kombinerar dem en 42-H induktans. Denna 42-H-induktor är parallell med 7-h-induktorn så att de kombineras för att ge


denna 6-h-induktor är i serie med 4-H och 8-H-induktorerna. Därför,
![]()
2. För kretsen i Figur.(4),
i(t) = 4(2 − e−10t) mA. Om i2(0) = -1 mA, hitta:
(a) i1(0);
(b) v(t), v1(t) och v2(t);
(c) I1(t) och I2 (t).

lösning:
(a) från i (t) = 4 (2−e-10t) mA, i(0) = 4(2 − 1) = 4 mamma.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(C) den nuvarande i1 erhålls som


på samma sätt,


Observera att I1(t) + I2(t) = i(t).