El tensor de Riemann (Schutz 1985) 
, también conocido como tensor de curvatura de Riemann-Christoffel (Weinberg 1972, p. 133; Arfken 1985, p. 123) o tensor de curvatura de Riemann (Misner et al. 1973, p. 218), es un tensor de cuatro índices que es útil en la relatividad general. Otros tensores relativistas generales importantes tales que el tensor de curvatura de Ricci y la curvatura escalar se pueden definir en términos de 
.
El tensor de Riemann es en cierto sentido el único tensor que se puede construir a partir del tensor métrico y sus derivados primero y segundo,
 |
(1)
|
donde 
son símbolos de Christoffel del primer tipo y 
es una derivada de coma (Schmutzer 1968, p. 108; Weinberg 1972). En una dimensión, 
. En cuatro dimensiones, hay 256 componentes. Haciendo uso de la simetría de las relaciones,
 |
(2)
|
el número de componentes independientes se reduce a 36. Uso de la condición
 |
(3)
|
el número de coordenadas se reduce a 21. Por último, utilizando
 |
(4)
|
20 se dejan componentes independientes (Misner et al. 1973, pp 220-221;Arfken 1985, 123-124).
En general, el número de componentes independientes en dimensiones 
viene dado por
 |
(5)
|
los «números piramidales de cuatro dimensiones», cuyos primeros valores son 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). El número de escalares que se pueden construir a partir de 
y 
es
 |
(6)
|
(Weinberg 1972). Los primeros valores son entonces 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).
En términos del tensor de Jacobi 
,
 |
(7)
|
Let
 |
(8)
|
donde la cantidad dentro de 
es un símbolo Christoffel de segundo tipo. Entonces
 |
(9)
|
se descompone en sus más simple descomposición en 
dimensiones,
 |
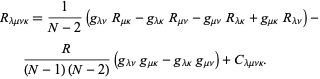(10)
|
Aquí, 
es el tensor de curvatura Ricci, 
es la curvatura escalar, y 
es el tensor de Weyl.